标签：调用 level for 感知器 style 连续 roc lib als
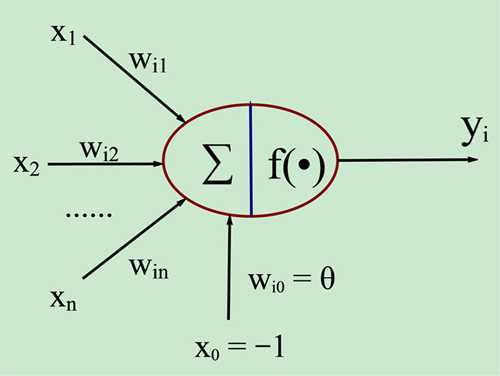
图中x1~xn是从其他神经元传来的输入信号，wij表示表示从神经元j到神经元i的连接权值，θ表示一个阈值 ( threshold )，或称为偏置( bias )。则神经元i的输出与输入的关系表示为：
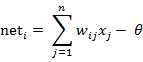
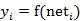
图中 yi表示神经元i的输出，函数f称为激活函数 ( Activation Function )或转移函数 ( Transfer Function ) ，net称为净激活(net activation)。若将阈值看成是神经元i的一个输入x0的权重wi0，则上面的式子可以简化为：
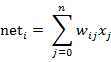
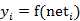
若用X表示输入向量，用W表示权重向量，即：
X = [ x0 , x1 , x2 , ....... , xn ]
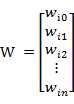
则神经元的输出可以表示为向量相乘的形式：
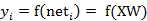
若神经元的净激活net为正，称该神经元处于激活状态或兴奋状态(fire)，若净激活net为负，则称神经元处于抑制状态。
图1中的这种“阈值加权和”的神经元模型称为M-P模型 ( McCulloch-Pitts Model )，也称为神经网络的一个处理单元( PE, Processing Element )。
激活函数的选择是构建神经网络过程中的重要环节，下面简要介绍常用的激活函数。
(1) 线性函数 ( Liner Function )
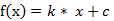
(2) 斜面函数 ( Ramp Function )
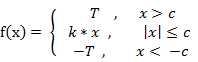
(3) 阈值函数 ( Threshold Function )
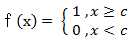
以上3个激活函数都属于线性函数，下面介绍两个常用的非线性激活函数。
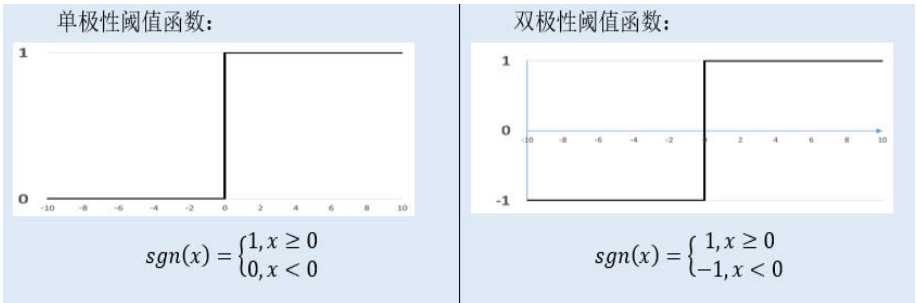
(4) S形函数 ( Sigmoid Function )
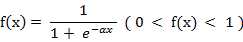
该函数的导函数：
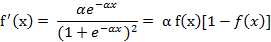
(5) 双极S形函数
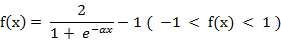
该函数的导函数：
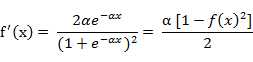
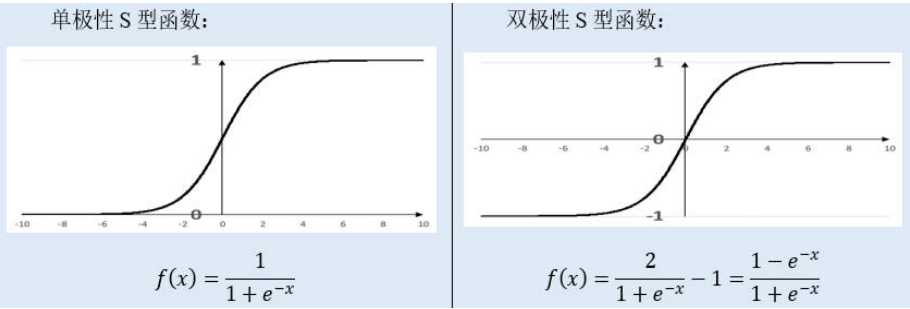
双极S形函数与S形函数主要区别在于函数的值域，双极S形函数值域是(-1,1)，而S形函数值域是(0,1)。
由于S形函数与双极S形函数都是可导的(导函数是连续函数)，因此适合用在BP神经网络中。（BP算法要求激活函数可导）
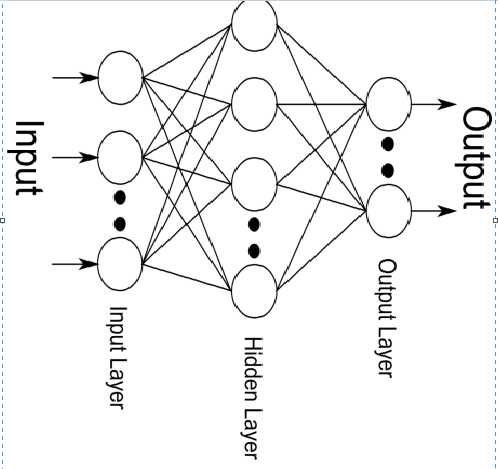
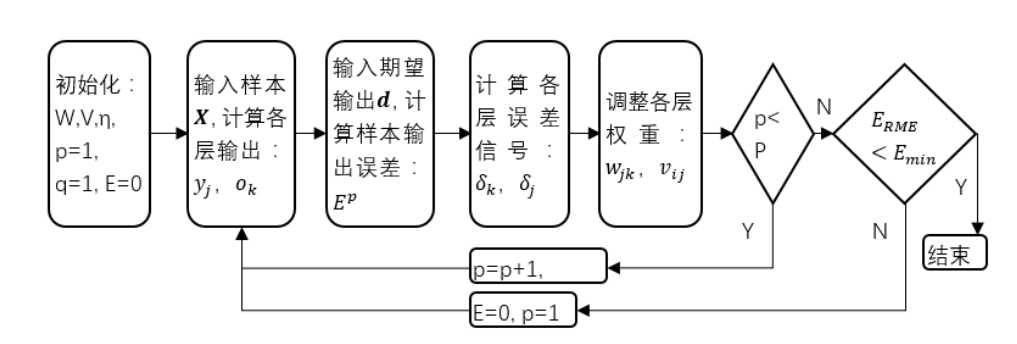
BP网络的学习过程由信号的正向传播和反向传播两个过程组成：
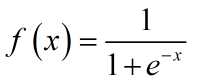
对于隐层：
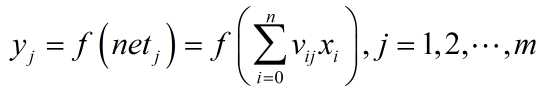
对于输出层：
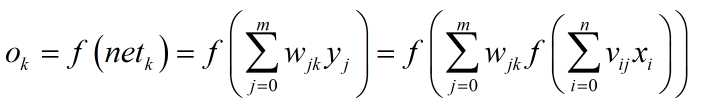
3.权值调整
这里我们用代价函数E来描述网络误差，使用随机梯度下降（SGD，StochasticGradient Descent）策略， 以代价函数的负梯度方向对参数进行调整。每次只针对一个训练样例更新权值。这种算法被称作误差逆传播（error Back Propagation）算法，简称标准BP算法
代价函数E：
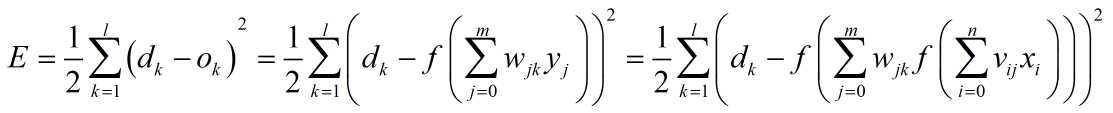
根据梯度下降策略，误差沿梯度方向下降最快，故应使权值的调整量与误差的梯度下降成正比，即：
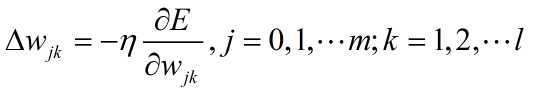
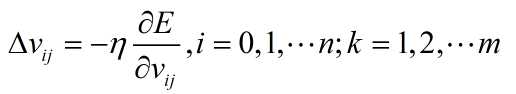
其中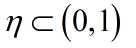
表示学习率，用来限制训练速度的快慢
*引入上一次的权值调整作为调整项，使权值调整具有一定的惯性，含有动量项的权值调整表达式为
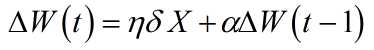
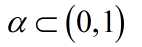称为动量因子。即此次权值的调整如果和上次方向相同会加速收敛，如果方向相反会减缓震荡。因此可以很好的提高训练速度
*学习率在一定程度上限定了权值调整的快慢, 学习率调整也是先用大的学习率到震荡区域，这个区域包含极小值，然后再用小的学习率逼近极小值。学习率的增减通过乘以一个因子来实现
清理环境变量，加载Soanr,Mines vs. Rocks 数据
rm(list=ls())
library(mlbench)
data(Sonar)
重新定义因子级别为0,1，其中岩石是级别1，金属是级别0
levels(Sonar$Class)<-c(0,1)
随机抽样，建立训练集和测试集,抽样比例是7:3
set.seed(1221) select<-sample(1:nrow(Sonar),nrow(Sonar)*0.7) train<-Sonar[select,] test<-Sonar[-select,]
对数据进行中心标准化
train[,1:60]=scale(train[,1:60]) test[,1:60]=scale(test[,1:60])
使用nnet包实现BP神经网络
library(nnet) mynnet<-nnet(Class~., linout =F,size=14, decay=0.0076, maxit=200, data = train)
结果评估
使用测试集预测
out<-predict(mynnet, test) out[out<0.5]=0 out[out>=0.5]=1
计算准确率
rate<-sum(out==test$Class)/length(test$Class)
分别在训练集和测试集上预测，并且绘制ROC曲线
ROC<-function(model,train,test,objcolname,ifplot=TRUE){ library(ROCR,quietly = T) train$p<-predict(model, train) test$p<-predict(model, test) predTr <- prediction(train$p, train[,objcolname]) perfTr <- performance(predTr,"tpr","fpr") predTe <- prediction(test$p, test[,objcolname]) perfTe <- performance(predTe,"tpr","fpr") tr_auc<-round(as.numeric(performance(predTr,‘auc‘)@y.values),3) te_auc<-round(as.numeric(performance(predTe,‘auc‘)@y.values),3) if(ifplot==T){ plot(perfTr,col=‘green‘,main="ROC of Models") plot(perfTe, col=‘black‘,lty=2,add=TRUE); abline(0,1,lty=2,col=‘red‘) tr_str<-paste("Tran-AUC:",tr_auc,sep="") legend(0.3,0.45,c(tr_str),2:8) te_str<-paste("Test-AUC:",te_auc,sep="") legend(0.3,0.25,c(te_str),2:8) } auc<-data.frame(tr_auc,te_auc) return(auc) }
ROC(model=mynnet,train=train,test=test,objcolname="Class",ifplot=T)
构建调参函数network()
network<-function(formula,data,size,adjust,decay=0,maxit=200,scale=TRUE, samplerate=0.7,seed=1,linout=FALSE,ifplot=TRUE){ library(nnet) ##规范输出变量为0,1 yvar<-colnames(data)==(all.vars(formula)[1]) levels(data[,yvar])<-c(0,1) ##抽样建立训练集和测试集 set.seed(seed) select<-sample(1:nrow(data),nrow(data)*samplerate) train=data[select,] test=data[-select,] ##根据给定判断进行标准化 if(scale==T){ xvar<-colnames(data)!=(all.vars(formula)[1]) train[,xvar]=scale(train[,xvar]) test[,xvar]=scale(test[,xvar]) } ##循环使用nnet训练调参 obj<-eval(parse(text = adjust)) auc<-data.frame() for(i in obj){ if(adjust=="size"){ mynnet<-nnet(formula,size=i,linout=linout,decay=decay, maxit=maxit,trace=FALSE,data=train) } else if(adjust=="decay"){ mynnet<-nnet(formula,size=size,linout=linout,decay=i, maxit=maxit,trace=FALSE,data=train) } ##调用之前的ROC()得到对应参数的AUC值 objcolname<-all.vars(formula)[1] auc0<-ROC(model=mynnet,train=train,test=test, objcolname=objcolname,ifplot=F) ##输出指定参数不同值对应的数据框 out<-data.frame(i,auc0) auc<-rbind(auc,out) } names(auc)<-c(adjust,"Train_auc","Test_auc") if(ifplot==T){ library(plotrix) twoord.plot(auc[,1],auc$Train_auc,auc[,1],auc$Test_auc,lcol=4, rcol=2,xlab=adjust,ylab="Train_auc", rylab="Test_auc",type=c("l","b"),lab=c(15,5,10)) } return(auc) }
开始调参
auc<-network(Class~.,data=Sonar,size=1:16,adjust="size", decay=0.0001,maxit=200,scale=T) auc<-network(Class~.,data=Sonar,size=14,adjust="decay", decay=c(0,seq(0.0001,0.01,0.0003)),maxit=200)
标签：调用 level for 感知器 style 连续 roc lib als
原文地址：http://www.cnblogs.com/karlpearson/p/6192821.html
