标签：联合 数据 一个人 概率图模型 style hmm 逻辑回归 复杂 但我
一、一些概念
互信息：
两个随机变量x和Y的互信息，定义X, Y的联合分布和独立分布乘积的相对熵。
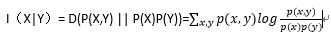
贝叶斯公式：
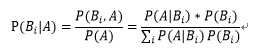
贝叶斯带来的思考：
给定某些样本D，在这些样本中计算某结论
出现的概率，即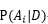
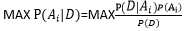给定样本D 所以可以推出
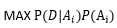，再假定p(Ai)相等，可以推出
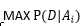，这个就是最大似然估计做的事情，看下取哪个参数
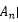的时候，D出现的概率最大，最大似然估计其实假定了任何参数被取到的概率都是一样的。
二、贝叶斯网络
随机变量之间并不是独立，而是存在复杂的网络关系。贝叶斯网络又称为有向无环图模型，是一个概率图模型（PGM），根据概率图的拓扑结构，考察一组随机随机变量{X1,X2…Xn}及其n组条件概率分布的性质。有向无环图中的节点表示随机变量，他们可以是观查到的变量，或隐变量、未知参数等。若两个节点间以一个单向箭头连接在一起，表示两个事件有关系，两节点就会产生一个条件概率值。马尔科夫网络是无向图网络。
一个简单的贝叶斯网络：
P(a, b, c)=P(c|a, b)P(b|a)P(a)
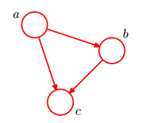
全连接贝叶斯网络：
每一对结点之间都有边连接，比如有5个结点就有=10条边。其实这种是我们最不希望看到的，因为这样建立的模型比较复杂。
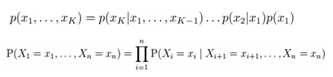
一个正常的贝叶斯网络：
有些边缺失，直观上X1和X2独立，X6和X7在X4给定的条件下独立。
X1，X2…X7的联合分布：
P(x1) P(x2) P(x3) P(x4|x1,x2,x3) P(x5|x1,x3) P(x6|x4) P(x7|x4,x5)
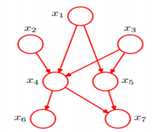
一个实际贝叶斯网络：
需要知道的参数个数为1+2+2+4+4=13 和全连接的2**5=32个相比少了一半。根据实际情况建立贝叶斯网络，可以减少大量参数。有可能实际中是知道一个人是否抽烟，知道x-ray和呼吸困难的情况，从而可以推断得肺癌和支气管炎的概率。
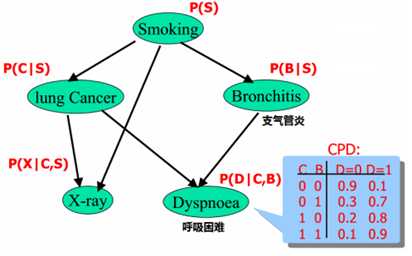
特殊的贝叶斯网络：
结点形成一条链式网络，称作马尔科夫模型。Ai+1只有Ai有关。有二阶马尔科夫网络、三阶马尔科夫网络，但我们往往不会去做那么高阶的马尔科夫网络，太复杂了。PLSA主题模型属于马尔科夫网络。
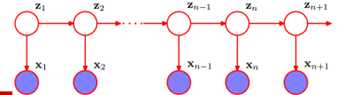
HMM:
假定z1、z2….zn+1（文字）是隐状态的，我们观察到的是x1、x2…xn+1（人说话的波形数据）
贝叶斯网络用处：
诊断：P（病因|症状）
预测：P（症状|病因）
贝叶斯网络的构建：
根据独立的条件，一条边一条边的试验，看是否能够连接。此过程可能中看不一定中用。如果有先验的知识，最好先按先验的知识建立贝叶斯网络。
混合网络（离散+连续）的构建：
隐马尔可夫里面就是混合网络。LDA是贝叶斯网络，都是离散的。
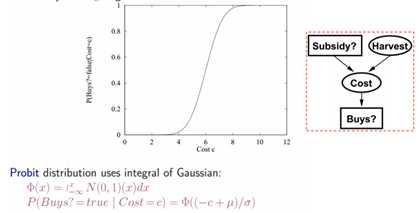
假设cost是服从正太分布的，当subsidy=true的时候有一个ath+bt的均值和方差，当subsidy=false的时候又有另一个ah+b的均值和方差。
然后buys是离散，cost是连续，那么又可以用逻辑回归建模。
标签：联合 数据 一个人 概率图模型 style hmm 逻辑回归 复杂 但我
原文地址：http://www.cnblogs.com/fionacai/p/6194566.html
