图像的点运算

对于一个数字图像处理系统来说， 一般可以将处理流程分为3个阶段。在获取原始图像
后， 首先是图像预处理阶段， 其次是特征抽取阶段，最后才是识别分析阶段。预处理阶段尤
为重要， 这个阶段处理不好则直接导致后面的工作无法展开。
点运算指的是对图像中的每个像素依次进行同样的灰度变换运算。设r和s分别是输入
图像f(x,y）和输出图像g(x,y）在任一点(x，y）的灰度值，则点运算可以使用下式定义

$$s=T(r)$$
其中， T为采用的点运算算子， 表示在原始图像和输出图像之间的某种灰度级映射
关系。
点运算常常用于改变图像的灰度范围及分布， 是图像数字化及图像显示时常常需要的工具． 点运算因其作用的性质有时也被称为对比度 增强、对比度拉伸或灰度变换。

本章主要包括以下内容

• 最基本的图像分析工具:灰度直方图
• 利用直方图辅助实现的各种灰度变换， 包括灰度线性变换、伽马变换、阀值变换和窗
  口变换等
• 两种实用的直方图修正技术:直方图均衡化和直方图规定化
• 本章的典型案例分析
  
  • 基于直方图均衡化的图像灰度归一化
  • 直方图匹配

灰度直方图

灰度直方圈描述了一幅图像的灰度级统计信息，主要应用于图像分割和图像灰度变换等
处理过程中．

理论基础
从数学角度来说，图像直方图描述图像各个灰度级的统计特性，它是图像灰度值的函数，
统计一幅图像中各个灰度级出现的次数或概率。有一种特殊的直方图叫做归一化直方图， 可
以直接反映不同灰皮级出现的比率。
从图形上来说， 灰度直方图是一个二维图， 横坐标为图像中各个像素点的灰度级别， 纵坐标表示具有各个灰度级别的像素在图像中出现的次数或概率。

matlab实现
Matlab中的imhist函数可以进行图像的灰度直方圈运算，调用语法为：

imhist(I)
imhist(I,n)
[count,x]=imhist(...)

• I为需要计算灰度直方图的图像．
  ? n为指定的灰度级数目． 如果指定参数n，则会将所有的灰度级均匀分布在n 个小区
  间内，而不是将所有的灰度级全部分开．
  ? counts为直方图数据向量. counts(i）表示第i个灰度区间中的像素数目．
  ? x是保存了对应的灰度小区间的向量．

若调用时不接收这个函数的返回值，贝Jj直接显示直方图：在得到这些返回数据之后，也
可以使用stem(x, count)来手工绘制直方图。

一般直方图

I = imread(‘pout.tif‘);
figure;
imshow(I); title(‘Souce‘);
figure;
imhist(I);title(‘Graph‘);
figure;
imhist(I,64);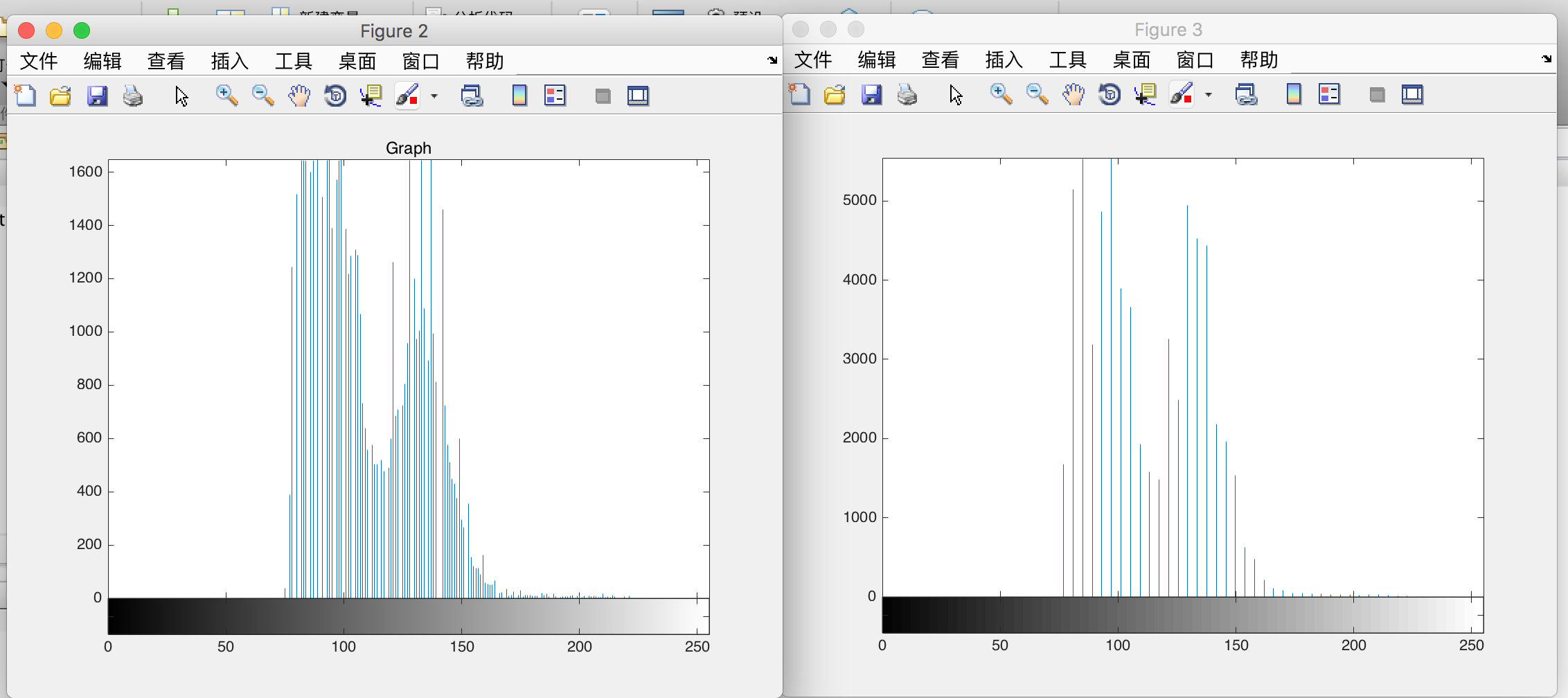

归一化直方图

在由imhist 函数的返回值中， counts 保存了落入每个区间的像素的个数， 通过计算 couts与图像中像素总数的商可以得到归一化的直方图。

I = imread(‘pout.tif‘);
figure;
[M,N]=size(I);
[counts,x]=imhist(I,32);
counts= counts / M/N;
stem(x,counts);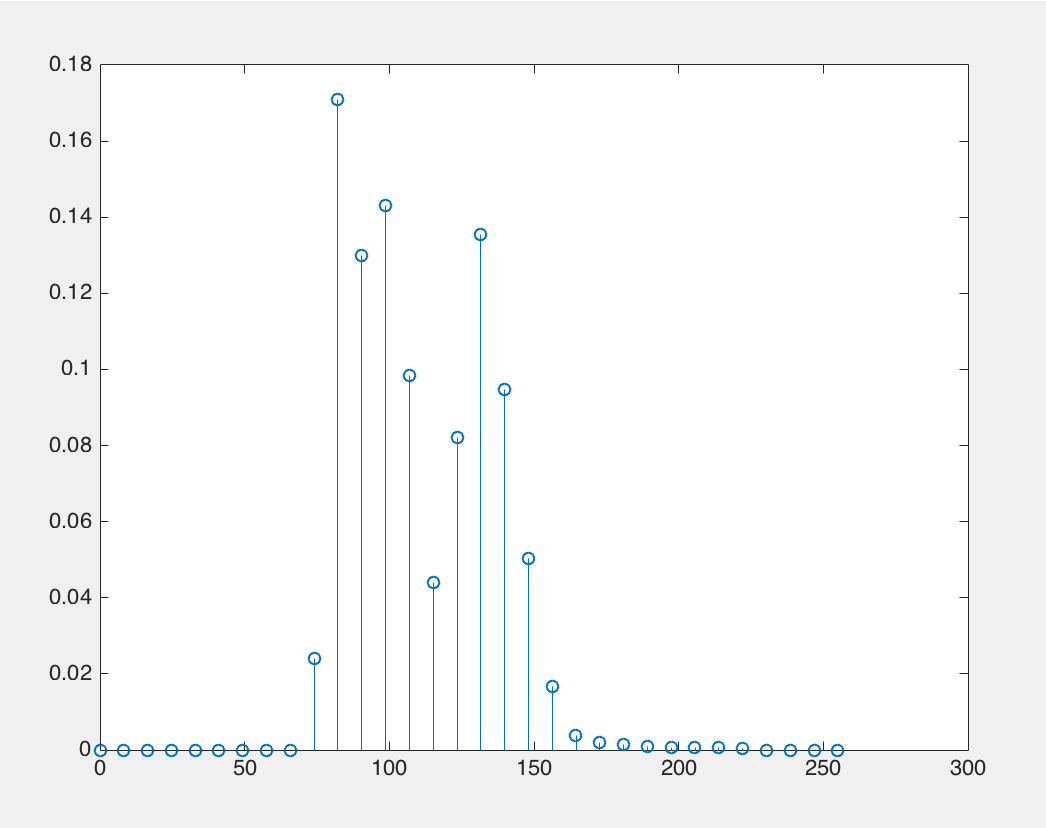

分析图像的灰度直方图往往可以得到很多有效的信息。 例如， 从图 3.4的一系列灰度直 方图上， 可以很直观地看出图像的亮度和对比度特征。 实际上， 直方图的峰值位置说明了图 像总体上的亮暗： 如果图像较亮， 则直方图的峰值出现在直方图的较右：部分：如果图像较暗．则直方图的峰值出现在直方图的较左部分， 从而造成暗部细节难以分辨。 如果直方图中只有中间某一小段非零值，贝IJ这张图像的对比度较低： 反之， 如果直方图的非零值分布很宽而且比较均匀， 则图像的对比度较高。

灰度的线性变换

线性灰度变换函数f(x）是一个一维线性函数：

$$D_B = f(D_A) ＝f_AD_A +f_B$$
式中参数$f_A$为线性函数的斜率， $f_B$为线性函数在y轴的截距， $D_A$ 表示输入图像的灰度，
$D_B$ 表示输出图像的灰度。

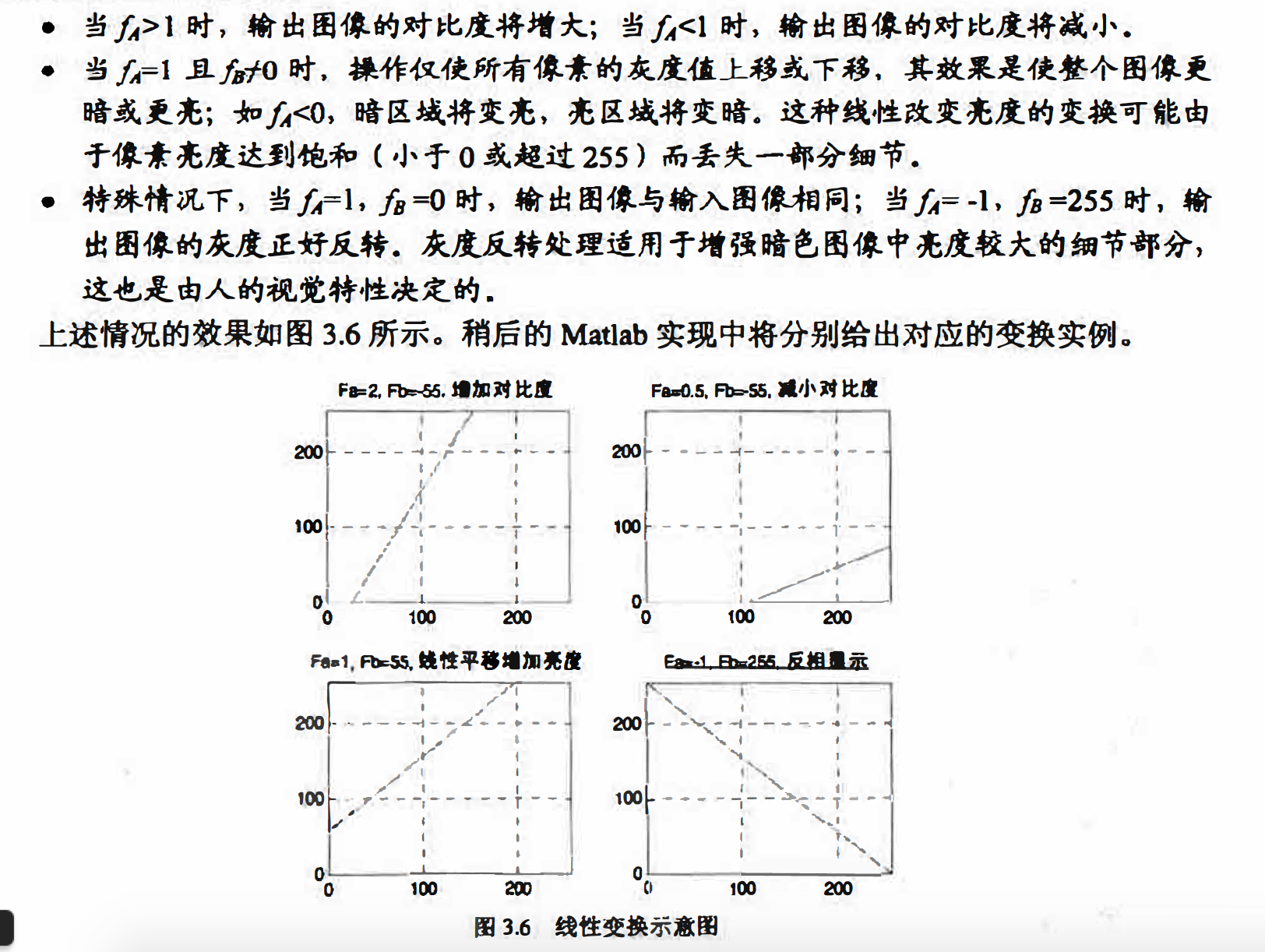
matlab实现
使用Matlab对图像执行线性变换无需专门的函数， 下面的程序对Matlab示例图像 coiilsJpg进行了不同参数的线性变换操作

I = imread(‘coins.png‘);        % 读入原图像

I = im2double(I);           % 转换数据类型为double
[M,N] = size(I);            % 计算图像面积

figure(1);              % 打开新窗口
imshow(I);              % 显示原图像
title(‘原图像‘);

figure(2);              % 打开新窗口
[H,x] = imhist(I, 64);      % 计算64个小区间的灰度直方图
stem(x, (H/M/N), ‘.‘);      % 显示原图像的直方图
title(‘原图像‘);

% 增加对比度
Fa = 2; Fb = -55;
O = Fa .* I + Fb/255;

figure(3);
subplot(2,2,1);
imshow(O);
title(‘Fa = 2 Fb = -55 增加对比度‘);

figure(4);
subplot(2,2,1);
[H,x] = imhist(O, 64);
stem(x, (H/M/N), ‘.‘);
title(‘Fa = 2 Fb = -55 增加对比度‘);

% 减小对比度
Fa = 0.5; Fb = -55;
O = Fa .* I + Fb/255;

figure(3);
subplot(2,2,2);
imshow(O);
title(‘Fa = 0.5 Fb = -55 减小对比度‘);

figure(4);
subplot(2,2,2);
[H,x] = imhist(O, 64);
stem(x, (H/M/N), ‘.‘);
title(‘Fa = 0.5 Fb = -55 减小对比度‘);

% 线性增加亮度
Fa = 1; Fb = 55;
O = Fa .* I + Fb/255;

figure(3);
subplot(2,2,3);
imshow(O);
title(‘Fa = 1 Fb = 55 线性平移增加亮度‘);

figure(4);
subplot(2,2,3);
[H,x] = imhist(O, 64);
stem(x, (H/M/N), ‘.‘);
title(‘Fa = 1 Fb = 55 线性平移增加亮度‘);

% 反相显示
Fa = -1; Fb = 255;
O = Fa .* I + Fb/255;

figure(3);
subplot(2,2,4);
imshow(O);
title(‘Fa = -1 Fb = 255 反相显示‘);

figure(4);
subplot(2,2,4);
[H,x] = imhist(O, 64);
stem(x, (H/M/N), ‘.‘);
title(‘Fa = -1 Fb = 255 反相显示‘);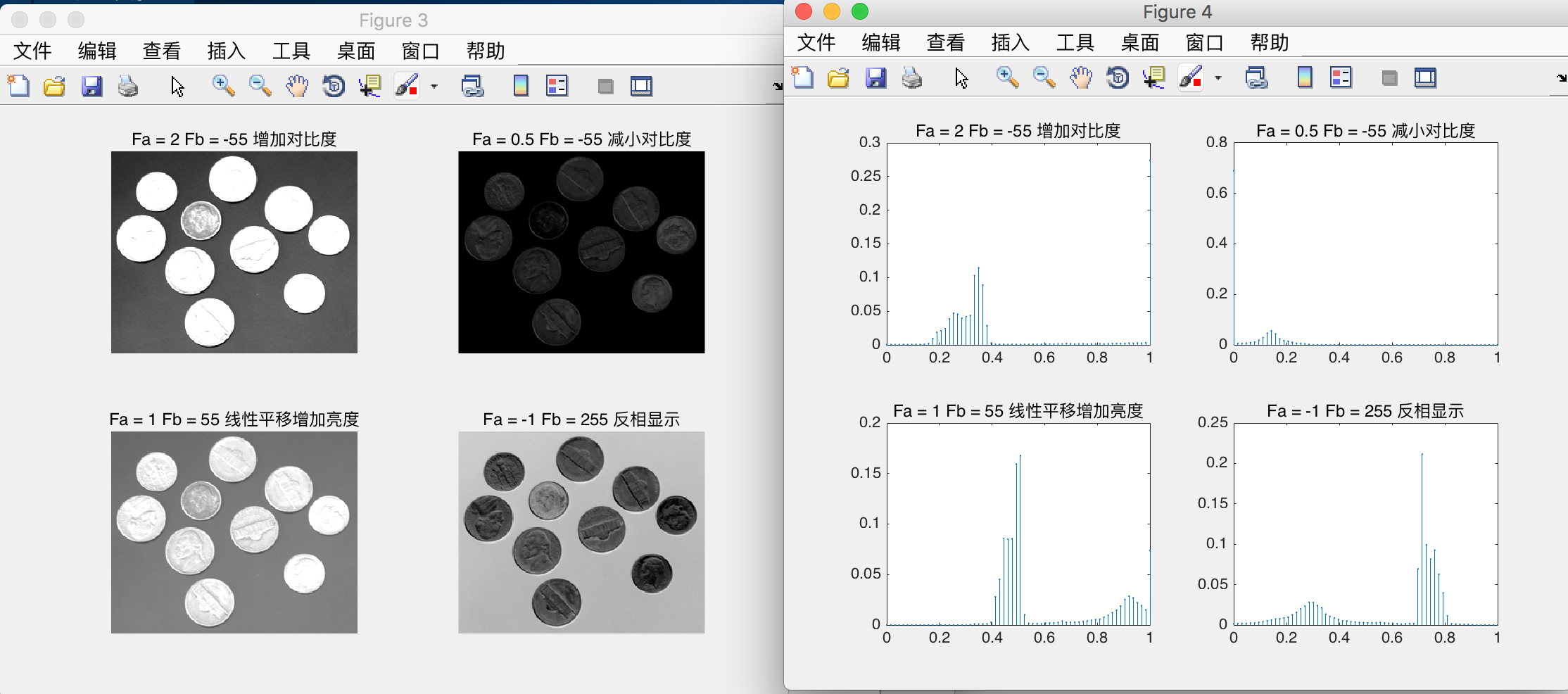

可以看出:改变图像的对比度是，对直方图的缩放与平移， 改变图像的亮度则只是平移直方图在横轴上的位置， 而反相则是将直方图水平镜像。
单纯的线性灰度变换可以在一定程度上解决视觉上的图像整体对比度问题， 但是对面像细节部分的增强则较为有限， 结合后面将要介绍的非线性变换技术可以解决这一问题．

灰度对数变换

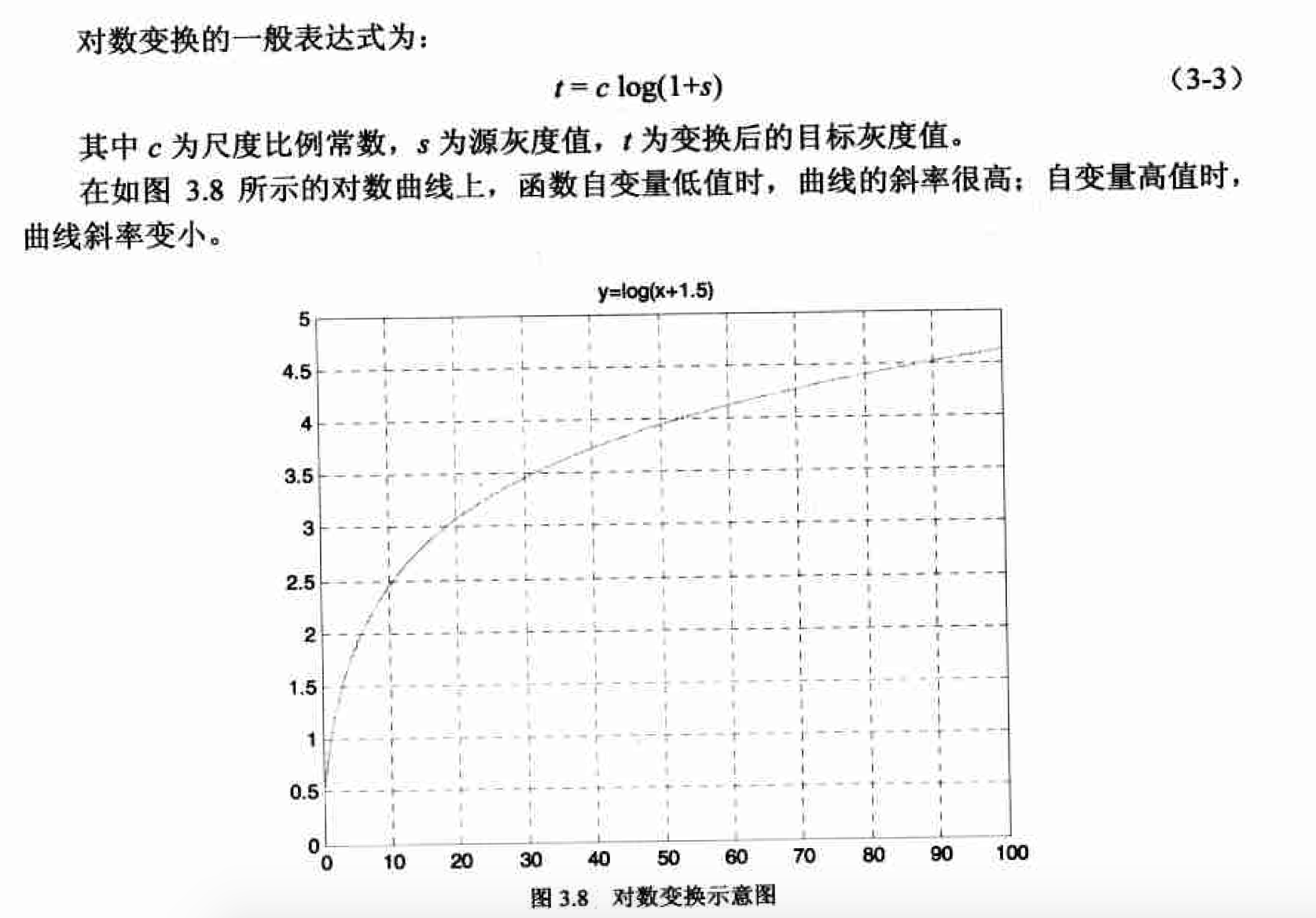
由对数函数曲线可知，这种变换可以增强一幅图像中较暗部分的细节，从而可用来扩展被压缩的高值图像中的较暗像素，因此对数变换被广泛地应用于频谱图像的显示中。一个典 型的应用是傅立叶频谱〈参见第6章〉，其动态范围可能宽达0～106.直接显示频谱时，图像显示设备的动态范围往往不能满足要求，从而丢失大量的暗部细节。而在使用对数变换之后，图像的动态范围被合理地非线性压缩，从而可以清晰地显示。本节的Matlab实现中就提供了一个这样的示例。

关于动态范围，对比度的解释
请问数字图像处理中的对比度是何含义?动态范围呢?

matlab实现
对数变换不需要专门的图像处理函数，可以使用如下数学函数实现对图像I的对数变换。
T = log(I + 1)_;

I = imread(‘coins.png‘);
F = fft2(im2double(I));
F = fftshift(F);
F = abs(F);
T = log(F+1);

subplot(1,2,1);
imshow(F,[]);
title(‘未经变换的频谱‘);

subplot(1,2,2);
imshow(T,[]);
title(‘对数变换后‘);

通过图3.9(a）中未经变换的频谱可见．图像中心绝对高灰度值的存在压缩了低灰度部分的动态范围，从而无法在显示时表现出细节：而经过对数灰度处理的图像，其低灰度区域 对比度将会增加，暗部细节被增强。

伽玛变换

伽玛变换又名指数变换或幂次变换，是另一种常用的灰度非线性变换。

伽玛变换的一般表达式为：

$$y=(x+esp)^{\gamma}$$
其中，x与y的取值范围均为［0,1］。esp为补偿系数，$\gamma$则为伽玛系数．

与对数变换不同，伽玛变换可以根据$\gamma$的不同取值选择性地增强低灰度区域的对比度或是高灰度区域的对比度。
$\gamma$是图像灰度校正中非常重要的一个参数，其取值决定了输入图像和输出。图像之间的灰度映射方式，即决定了是增强低灰度（阴影区域〉还是增强高灰度（高亮区域):

• y>1时，图像的高灰度区域对比度得到增强；
• y<1时，图像的低灰皮区域对比度得到增强；
• y=1时，这一灰度变换是线性的，即不改变原图像．

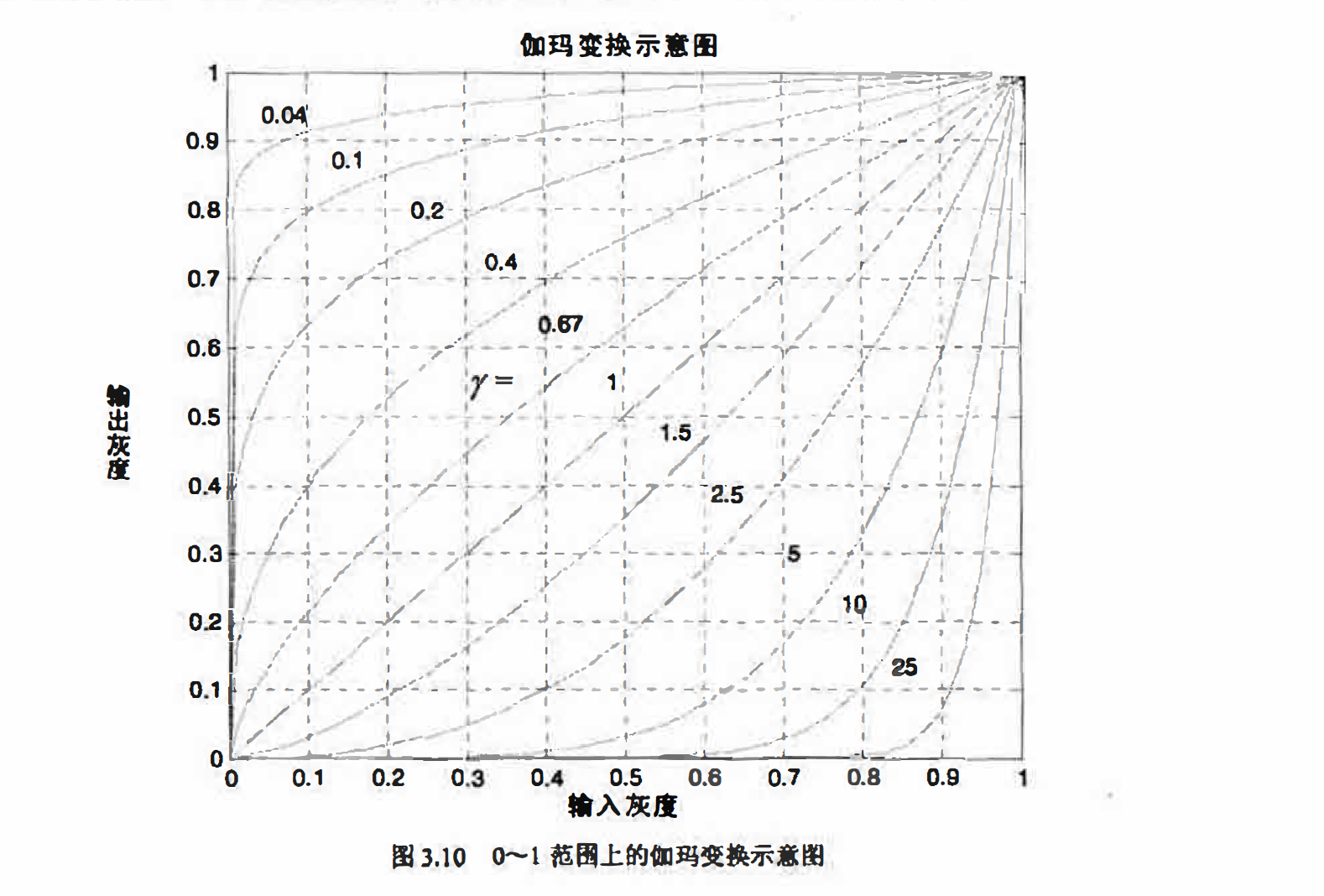
伽玛变换的映射关系如图3.10所示。在进行变换时，通常需要将0～255的灰图动态范围首先变换到0～1的动态施围，然后执行伽玛变换后再恢复原动态范围。

matlab实现
Matlab中提供了实现灰度变换的基本工具imadust它有着非常广泛的用途，其调用的 一般语法为：

注意
当$\gamma<1$时则映射被加权至更高输出值，当$\gamma>1$则映射被加权至更低输出值。

下面给出了gamma分别取不同值时的伽玛变换的程序实现：

I = imread(‘pout.tif‘);

subplot(1,3,1);
imshow(imadjust(I,[],[],0.75));
title(‘Gamma 0.75‘);

subplot(1,3,2);
imshow(imadjust(I,[],[],1));
title(‘Gamma 1‘);

subplot(1,3,3);
imshow(imadjust(I,[],[],1.5));
title(‘Gamma 1.5‘);

上述程序的运行结果如图 3.11 所示，可以看出不同伽玛因子给图像的整体明暗程度带来 的变化，以及对图像暗部和亮部细节清晰度的影响。当伽玛因子取 1 的时候，图像没有任何改变。

下面的程序生成了图3.12中3幅图像的灰直方图。

I = imread(‘pout.tif‘);

subplot(1,3,1);
imhist(imadjust(I,[],[],0.75));
title(‘Gamma 0.75‘);

subplot(1,3,2);
imhist(imadjust(I,[],[],1));
title(‘Gamma 1‘);

subplot(1,3,3);
imhist(imadjust(I,[],[],1.5));
title(‘Gamma 1.5‘);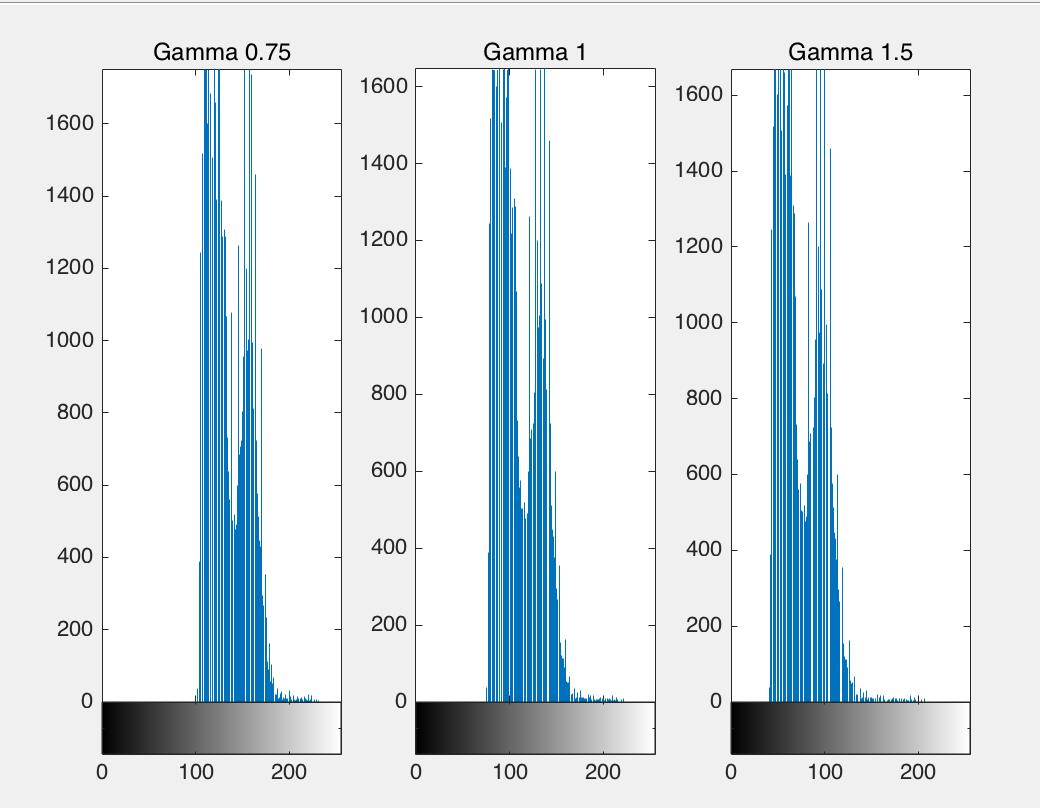

注意图3.12中直方图非零区间位置的变化，以及这些变化给图像带来的影响。由于伽玛 变换并不是线性变换，所以它不仅可以改变图像的对比度，还能够增强细节，从而带来整体 图像效果的改善。

灰度阙值变换

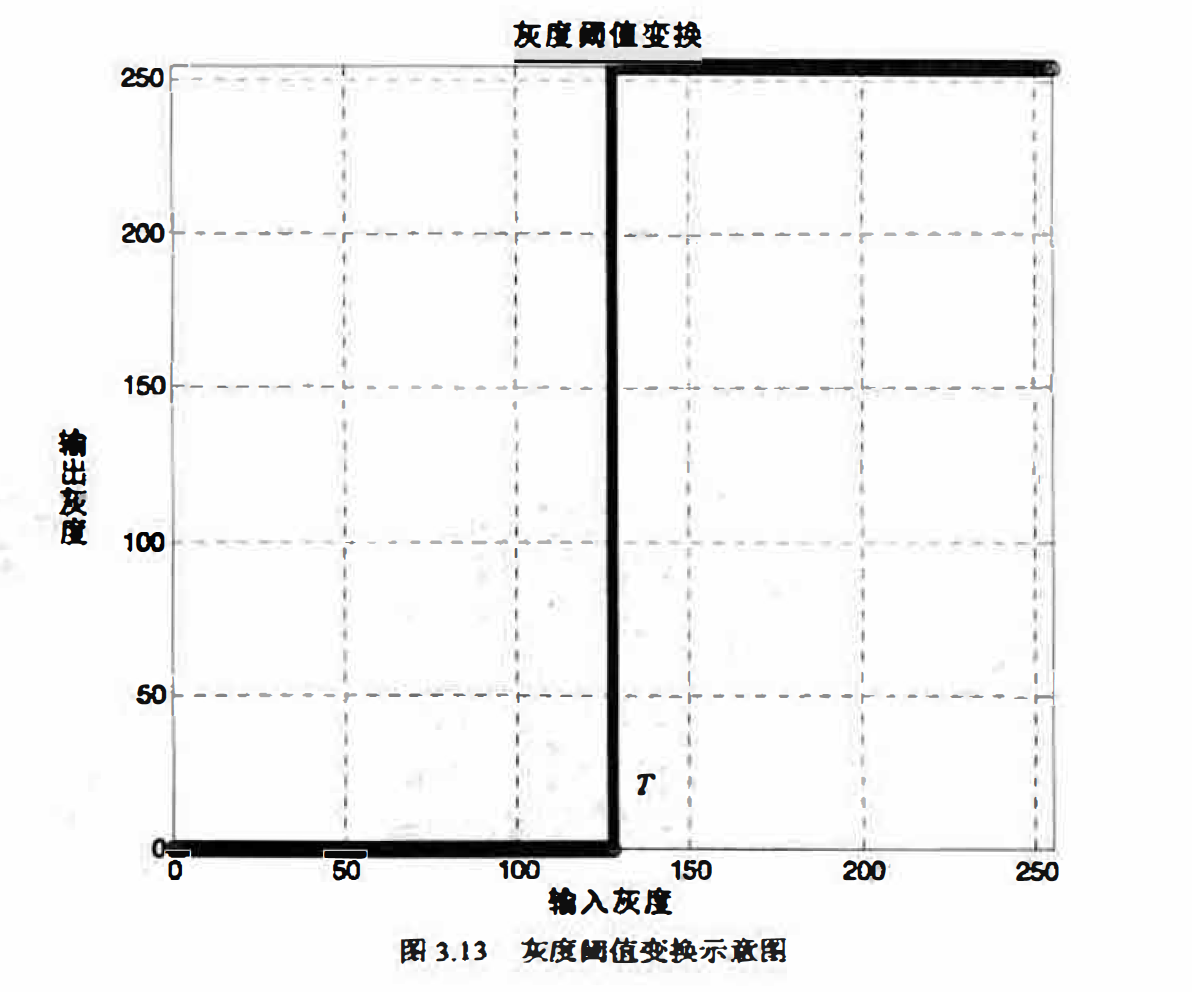
灰度阙值变换可以将一幅灰度图像转换成黑白的二值图像。用户指定一个起到分界线作用的灰度值，如果图像中某像素的灰度值小于该灰度值，则将该像素的灰度值设置为0，否 则设置为255；.这个起到分界线作用的灰度值称为阙值，灰度的阙值变换也常被称为阀值化， 或二值化。

将图像内容直接划分为我们关心的和不关心的2个部分，从而在复杂背景中直接提取出感兴趣的目标。因此它是图像分割的重要手段之一，这一点在第9章中还将进一步阐述。

matlab实现

I = imread(‘rice.png‘);
thresh = graythresh(I);
bw1=im2bw(I,thresh);
bw2=im2bw(I,130/255);
subplot(1,3,1);
imshow(I);
title(‘原图像‘);

subplot(1,3,2);
imshow(bw1);
title(‘自动选择阀值‘);   

subplot(1,3,3);
imshow(bw2);
title(‘阀值130‘); 

由图可见，单纯的灰度阀值化无法很好地处理灰度变化较为复杂的图 像，常常给物体的边缘带来误差，或者给整个画面带来噪点。此时需要通过其他的图像处理 手段予以弥补，我们将在 8.4 节介绍相关的内容．