标签:分享 div int ntp span 节点 ptr blog bool
满二叉树:一颗深度为k且有2^k-1个节点的二叉树称为满二叉树;
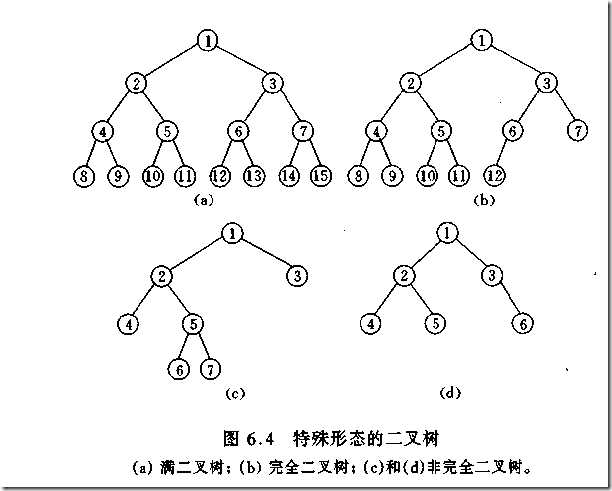
完全二叉树:对满二叉树的结点进行连续编号,约定编号从根结点起,自上而下,自左至右。深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树编号从1至n的结点对应时,称为完全二叉树。如图所示:
 1. 判定完全二叉树。判定一棵树是不是完全二叉树的思路是广度遍历该二叉树,当出现NULL值时停止遍历,如果此时还有没有遍历到的结点,那么就说明该树非完全二叉树,因为有空洞。C++代码如下:
1. 判定完全二叉树。判定一棵树是不是完全二叉树的思路是广度遍历该二叉树,当出现NULL值时停止遍历,如果此时还有没有遍历到的结点,那么就说明该树非完全二叉树,因为有空洞。C++代码如下:
#include "stdafx.h" #include <list> using namespace std; struct Tree{ Tree() { data = 0; pLeftChild = NULL; pRightChild = NULL; } int data; Tree* pLeftChild; Tree* pRightChild; }; Tree* GetFrontPtr(std::list<Tree*> &q) { if (q.empty()) { return NULL; } else { Tree* pRet = q.front(); q.pop_front(); return pRet; } return NULL; } bool IsCompleteTree(Tree *pRoot) { std::list<Tree*> q; Tree *ptr; q.push_back(pRoot); while ((ptr = GetFrontPtr(q)) != NULL) { q.push_back(ptr->pLeftChild); q.push_back(ptr->pRightChild); } while (!q.empty()) { ptr = q.front(); q.pop_front(); if (NULL != ptr) { return false; } } return true; } int _tmain(int argc, _TCHAR* argv[]) { Tree t1; Tree t2; Tree t3; Tree t4; Tree t5; Tree t6; Tree t7; Tree t8; Tree t9; Tree t10; t1.pLeftChild = &t2; t1.pRightChild = &t3; t2.pLeftChild = &t4; t2.pRightChild = &t5; t3.pLeftChild = &t6; bool ret = IsCompleteTree(&t1); return 0; }
2. 判定满二叉树。判定一棵树是否是满二叉树的思路类似,还是首先将二叉树按照广度优先的方法push到队列里边(暂时不pop),然后按照开始pop,第一次pop,只pop一个元素,第二次pop1*2个元素,第三次pop1*2*2个元素,依次类推,如果该pop1*2^k个元素,但是还没有pop完,list就空了,那么证明该树为非满二叉树。代码就不贴了。
标签:分享 div int ntp span 节点 ptr blog bool
原文地址:http://www.cnblogs.com/jiayayao/p/6218864.html