标签:ret empty src 思路 条件 判断 pop 输出 i++
在有向图G 中,每条边的长度均为1 ,现给定起点和终点,请你在图中找一条从起点到终点的路径,该路径满足以下条件:
1 .路径上的所有点的出边所指向的点都直接或间接与终点连通。
2 .在满足条件1 的情况下使路径最短。
注意:图G 中可能存在重边和自环,题目保证终点没有出边。
请你输出符合条件的路径的长度。
输入格式:
输入文件名为road .in。
第一行有两个用一个空格隔开的整数n 和m ,表示图有n 个点和m 条边。
接下来的m 行每行2 个整数x 、y ,之间用一个空格隔开,表示有一条边从点x 指向点y 。
最后一行有两个用一个空格隔开的整数s 、t ,表示起点为s ,终点为t 。
输出格式:
输出文件名为road .out 。
输出只有一行,包含一个整数,表示满足题目?述的最短路径的长度。如果这样的路径不存在,输出- 1 。
3 2
1 2
2 1
1 3
-1
6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5
3
解释1:
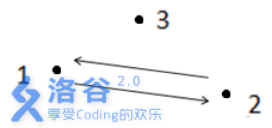
如上图所示,箭头表示有向道路,圆点表示城市。起点1 与终点3 不连通,所以满足题
目?述的路径不存在,故输出- 1 。
解释2:
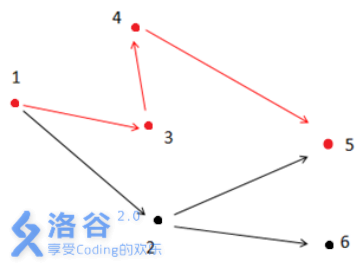
如上图所示,满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中,因为点2连了一条边到点6 ,而点6 不与终点5 连通。
对于30%的数据,0<n≤10,0<m≤20;
对于60%的数据,0<n≤100,0<m≤2000;
对于100%的数据,0<n≤10,000,0<m≤200,000,0<x,y,s,t≤n,x≠t。
1 #include<iostream>
2 #include<cstdio>
3 #include<cmath>
4 #include<cstring>
5 #include<queue>
6 using namespace std;
7 int head[500000];
8 int ct=0,s,t;
9 int used[300000],dis[300000],vis[300000];
10 int n,m,x[300000],y[300000];
11 bool flag;
12 struct edge{
13 int next;
14 int to;
15 }e[500000];
16 void add(int from,int to){
17 e[++ct].to=to;
18 e[ct].next=head[from];
19 head[from]=ct;
20 return;
21 }
22 bool pd(int pos){
23 int i;
24 for(i=head[pos];i;i=e[i].next){
25 if(!used[e[i].to])return 0;//未与终点联通
26 }
27 return 1;
28 }
29 void BFS()
30 {
31 queue<int>q;
32 q.push(t);used[t]=1;
33 while(!q.empty()){
34 int pos=q.front();q.pop();
35 for(int i=head[pos];i;i=e[i].next){
36 if(!used[e[i].to]){
37 q.push(e[i].to);
38 used[e[i].to]=1;
39 }
40 }
41 }
42 }
43 void SPFA()
44 {
45 queue<int> q;
46 q.push(s);dis[s]=0;vis[s]=1;
47 while(!q.empty()){
48 int p=q.front();vis[p]=0;q.pop();
49 if(pd(p)==0) continue;
50 for(int i=head[p];i;i=e[i].next){
51 int v=e[i].to;
52 if(dis[v]>dis[p]+1){
53 dis[v]=dis[p]+1;
54 if(!vis[v]){
55 q.push(v);vis[v]=1;
56 }
57 if(v==t){ flag=true; }
58 }
59 }
60 }
61 }
62 int main(){
63 scanf("%d%d",&n,&m);
64 int i,j;
65 for(i=1;i<=m;i++){
66 scanf("%d%d",&x[i],&y[i]);
67 add(y[i],x[i]);//第一遍反向制表
68 }
69 scanf("%d%d",&s,&t);
70 BFS();
71 if(!used[s]){
72 printf("-1");
73 return 0;
74 }
75 memset(head,0,sizeof(head));//再次初始化
76 memset(dis,0x3f,sizeof(dis));memset(vis,0,sizeof(vis));
77 ct=0;
78 for(i=1;i<=m;i++){
79 add(x[i],y[i]);
80 }
81 SPFA();
82 if(flag==false) printf("-1");
83 else printf("%d",dis[t]);
84 return 0;
85 }
思路:先建一张反向图,并且从终点反向BFS这时候将所有都到的点用used标记一下,然后再见一张正向图跑一边SPFA注意跑的时候判断一下,如果有一个点在反向BFS的时候没有用到,也就是used没标记,那么这个电是不也以用的,直接continue掉,求得dis[t]即为解
温馨提示:此题可以如上解法,也可以直接建两张图,重点来了,这是你要开两个head数组,不要像我似的,正向图、反向图用了一个head.
标签:ret empty src 思路 条件 判断 pop 输出 i++
原文地址:http://www.cnblogs.com/suishiguang/p/6219167.html