标签:.com 导出 存在 部分 多边形 思路 技术分享 title souya
对于定积分,高中教材里有如下引例:
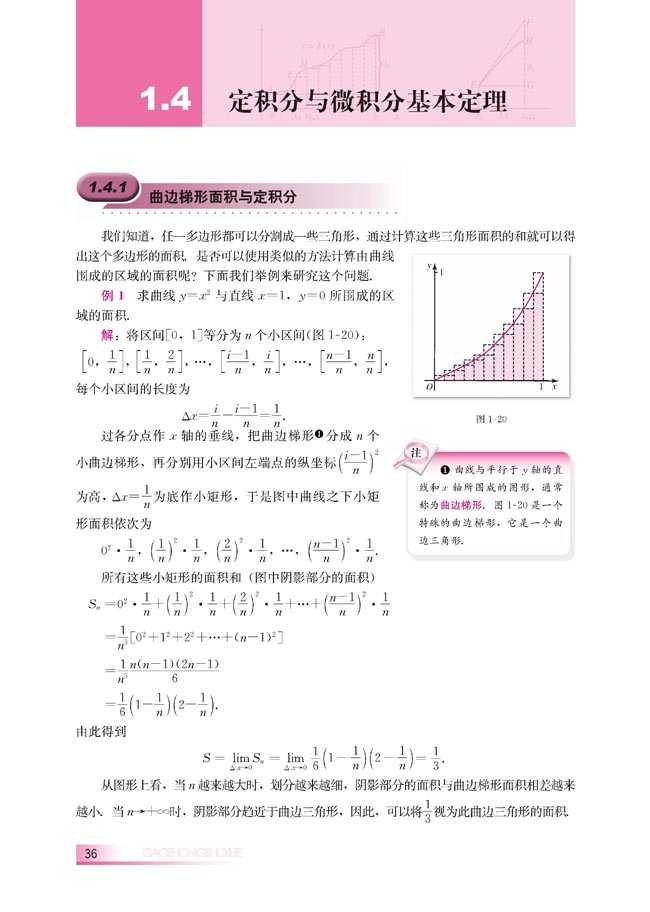
(高中教材本身就不严谨,这无所谓,但是我对这个例题印象太深了,所以拿它举例说明问题)
小矩形面积和的极限,等不等于曲线下方的面积?这是一个很迷的问题。
有人会说,面积不就是用积分定义的吗?可是你怎么保证你这样定义的面积跟几何直观上是一致的呢?
换句话说,图中小矩形面积之和,从几何直观上来看,是小于曲线下方的面积的。(整体大于部分)
如果极限存在,那么这个极限(也就是 \(\frac{1}{3}\))可能等于曲线下方的面积,也可能小于曲线下方的面积。(即不大于曲线下方的面积)
你怎么知道它就是等于,不是小于呢?
其实是可以证明它是等于的。这里要借用一下古希腊阿基米德的方法。
在遥远的古希腊,根本没有微积分的概念。但是阿基米德还是用微积分的思想严格导出了圆的面积和球的体积的公式。
他是如何保证严格的呢?思路是这样的。比如说现在要求圆的面积,就先证明圆内接正多边形的面积小于 \(\pi r^2\) 且收敛于圆的面积,再证明圆外接正多边形的面积大于 \(\pi r^2\) 且收敛于圆的面积。这样,如果假设圆的面积大于 \(\pi r^2\) 就跟第一条矛盾;如果假设圆的面积小于 \(\pi r^2\) 就跟第二条矛盾。所以圆的面积就只能是 \(\pi r^2\).
按照这个思路,我们已经得出了极限不大于曲线下方的面积,所以只需要再证该极限值不小于曲线下方的面积即可。
取每个小区间右端点的函数值作为小矩形的高并对面积(图中虚线包含的部分)求和,再取极限,同样会得到 \(\frac{1}{3}\) (注意这跟用前一种取高方法求出的极限是相等的). 而且此时小矩形的面积和从几何直观上看是大于曲线下方的面积的,所以极限 \(\frac{1}{3}\) 是不小于曲线下方的面积的。结合上面一点(极限 \(\frac{1}{3}\) 不大于曲线下方的面积)可知,该极限一定等于曲线下方的面积。这就从几何直观上把积分和面积对应起来了。
由此就可以得出,「可积」的意思就是可以用积分的方法求面积。因为可积的第一充要条件说,上和与下和的极限相等就可积(反过来也成立),而且这个极限就等于积分的值。
这就相当于是在说:上和不小于面积,下和不大于面积,极限又一致,所以极限就等于面积。如果极限不一致,就不能用这种方法求出面积。
标签:.com 导出 存在 部分 多边形 思路 技术分享 title souya
原文地址:http://www.cnblogs.com/li-hua/p/6219184.html