标签:abs poi point 距离 else div line wap int
计算几何凸包
凸包:给你n个散落的点,让你求出最小的凸多边形将所有的点包括起来,或者点在边上。用到的算法是Graham
Graham算法:首先找到一个顶点作为基点,然后将这个点与其他点进行连线,然后按照角度的大小进行排序。
然后加点,第一个点肯定在凸多边形上,然后开始加点,每加一个点,要用向量的×积判断以前是不是有边在他的里面,如果有的话,就将这个点替换,这个过程是一个回溯的过程
首先找基点,纵坐标最小的一定在凸包上,如果纵坐标相等那么就选横坐标小的。
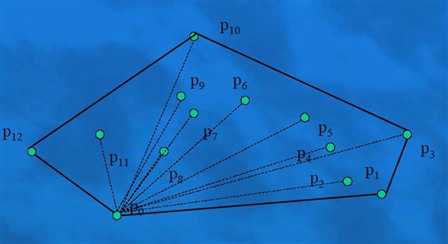
下面模拟一下Graham算法扫描的过程(截图来自HDU课件)
首相找到基点,很明显p0一定会在凸包上

然后将p0与其他各点相连,按照角度进行排序,排序的时候,不用求出来具体的角度,只需要利用向量的差乘的大小进行排序即可,然后按照角度的顺序进行加点
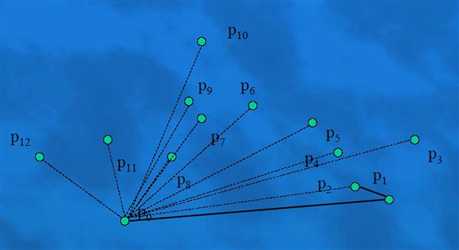
当加点p3后,发现向量p1p3在向量p2p3的外面,所以p2这个点肯定不在凸包上,所以删掉(这个过程是一个回溯的过程)
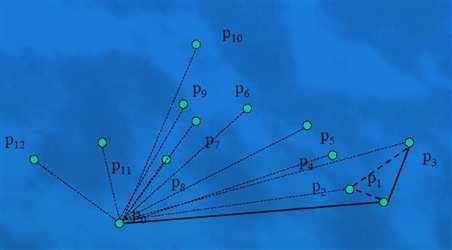
然后加点p4没有边在p3p4的外面,继续
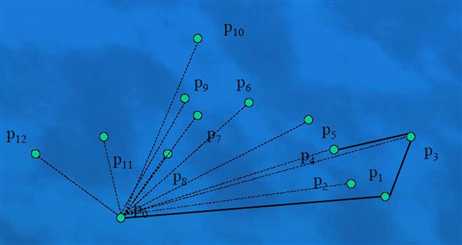
加p5的时候,p3p5在p4p5的外面,所以p4这个点也不在凸包上面删掉
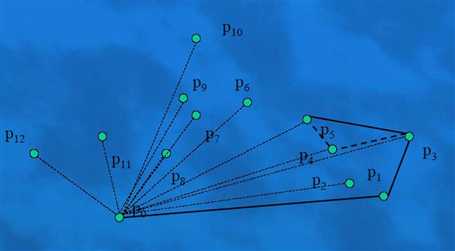
重复这个过程每次加点的时候,先要回溯一边,又没有边在要加的这条边的外面
……
最后找到了凸包
那用代码怎么来实现呐?
模板:
/****************************凸包模板*******************************/ const double eps = 1e-8; int sgn(double x) { if(fabs(x) < eps)return 0; if(x < 0)return -1; else return 1; } struct Point { double x,y; Point(){} Point(double _x,double _y) { x = _x;y = _y; } Point operator -(const Point &b)const { return Point(x - b.x,y - b.y); } //叉积 double operator ^(const Point &b)const { return x*b.y - y*b.x; } //点积 double operator *(const Point &b)const { return x*b.x + y*b.y; } void input(){ scanf("%lf%lf",&x,&y); } }; struct Line { Point s,e; Line(){} Line(Point _s,Point _e) { s = _s; e = _e; } }; //*两点间距离 double dist(Point a,Point b) { return sqrt((a-b)*(a-b)); } /* * 求凸包,Graham算法 * 点的编号0~n-1 * 返回凸包结果Stack[0~top-1]为凸包的编号 */ const int MAXN = 1010; Point List[MAXN]; int Stack[MAXN];//用来存放凸包的点 int top;//表示凸包中点的个数 //相对于List[0]的极角排序 bool _cmp(Point p1,Point p2) { double tmp = (p1-List[0])^(p2-List[0]); if(sgn(tmp) > 0) return true; else if(sgn(tmp) == 0 && sgn(dist(p1,List[0]) - dist(p2,List[0])) <= 0) return true; else return false; } void Graham(int n) { Point p0; int k = 0; p0 = List[0]; //找最下边的一个点 for(int i = 1;i < n;i++) { if( (p0.y > List[i].y) || (p0.y == List[i].y && p0.x > List[i].x) ) { p0 = List[i]; k = i; } } swap(List[k],List[0]); sort(List+1,List+n,_cmp); if(n == 1) { top = 1; Stack[0] = 0; return; } if(n == 2) { top = 2; Stack[0] = 0; Stack[1] = 1; return ; } Stack[0] = 0; Stack[1] = 1; top = 2; for(int i = 2;i < n;i++) { while(top > 1 && sgn((List[Stack[top-1]]-List[Stack[top-2]])^(List[i]-List[Stack[top-2]])) <= 0) top--; Stack[top++] = i; } } /****************************凸包模板*******************************/
标签:abs poi point 距离 else div line wap int
原文地址:http://www.cnblogs.com/wuwangchuxin0924/p/6223152.html