标签：stat guid ota asi res imp cti books abi
http://mathworld.wolfram.com/Variance.html
For a single variate 
having a distribution 
with known population mean 
, the population variance 
, commonly also written 
, is defined as
 |
(1)
|
where 
is the population mean and 
denotes the expectation value of 
. For a discrete distribution with 
possible values of 
, the population variance is therefore
 |
(2)
|
whereas for a continuous distribution, it is given by
 |
(3)
|
The variance is therefore equal to the second central moment 
.
Note that some care is needed in interpreting 
as a variance, since the symbol 
is also commonly used as a parameter related to but not equivalent to the square root of the variance, for example in the log normal distribution, Maxwell distribution, and Rayleigh distribution.
If the underlying distribution is not known, then the sample variance may be computed as
 |
(4)
|
where 
is the sample mean.
Note that the sample variance 
defined above is not an unbiased estimator for the population variance 
. In order to obtain an unbiased estimator for 
, it is necessary to instead define a "bias-corrected sample variance"
 |
(5)
|
The distinction between 
and 
is a common source of confusion, and extreme care should be exercised when consulting the literature to determine which convention is in use, especially since the uninformative notation 
is commonly used for both. The bias-corrected sample variance 
for a list of data is implemented as Variance[list].
The square root of the variance is known as the standard deviation.
The reason that 
gives a biased estimator of the population variance is that two free parameters 
and 
are actually being estimated from the data itself. In such cases, it is appropriate to use a Student‘s t-distribution instead of a normal distribution as a model since, very loosely speaking, Student‘s t-distribution is the "best" that can be done without knowing 
.
Formally, in order to estimate the population variance 
from a sample of 
elements with a priori unknown mean (i.e., the mean is estimated from the sample itself), we need an unbiased estimator for 
. This is given by the k-statistic 
, where
 |
(6)
|
and 
is the sample variance uncorrected for bias.
It turns out that the quantity 
has a chi-squared distribution.
For set of data 
, the variance of the data obtained by a linear transformation is given by
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
For multiple variables, the variance is given using the definition of covariance,
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
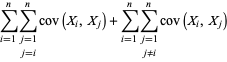(15)
|
 |
 |
 |
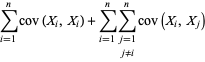(16)
|
 |
 |
 |
(17)
|
A linear sum has a similar form:
 |
 |
 |
(18)
|
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
These equations can be expressed using the covariance matrix.
SEE ALSO: Central Moment, Charlier‘s Check, Covariance, Covariance Matrix, Error Propagation, k-Statistic, Mean, Moment, Raw Moment, Sample Variance, Sample Variance Computation, Sample Variance Distribution, Sigma, Standard Error, Statistical Correlation
REFERENCES:
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 144-145, 1984.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Moments of a Distribution: Mean, Variance, Skewness, and So Forth." §14.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 604-609, 1992.
Roberts, M. J. and Riccardo, R. A Student‘s Guide to Analysis of Variance. London: Routledge, 1999.
标签：stat guid ota asi res imp cti books abi
原文地址：http://www.cnblogs.com/yuanjiangw/p/6236704.html
