标签:cti eth 不同 技术 nbsp 上界 等于 point 分享
前边由Hoeffding出发讨论了为什么机器可以学习,主要就是在N很大的时候Ein PAC Eout,选择较小的Ein,这样的Eout也较小,但是当时还有一个问题没有解决,就是当时的假设的h的集合是个数是有限的,那么本文继续讨论h个数为无限的情况。http://www.cnblogs.com/futurehau/p/6235348.html
其实之前的问题可以分类两个方面:
一方面:Ein 是否约等于 Eout
另一方面:Ein时候足够小。

所以,选择合适的M是很重要的,现在加入M为无限大的情况呢?
我们接下来的工作,就是想办法使用某个有限的mh来代替那个无限的M

之前我们让h可以自由选择的时候是让概率直接相加找上界,这样当M个数为无穷的时候,上界就比1还大了,这个对Ein和Eout的差距的控制就没有意义了。其实,这是由于扩充得太猛了,接下来一步步分析不要进行那么猛的扩充。
不同的h对于的坏数据可能是有许多重复的。

所以我们接下来考虑不同的分类场景下有多少种不同种类的分界线(超平面)
假设用一条线来分类二维平面上的数据集,那么点的数目和线的种类关系如下:

这样,如果effective(N)可以代替M,并且effective(N)<< 2^N,那么似乎就是可以学习的了
假设不是一条线分开,而是超平面的话:


那么,怎么计算增长函数呢?
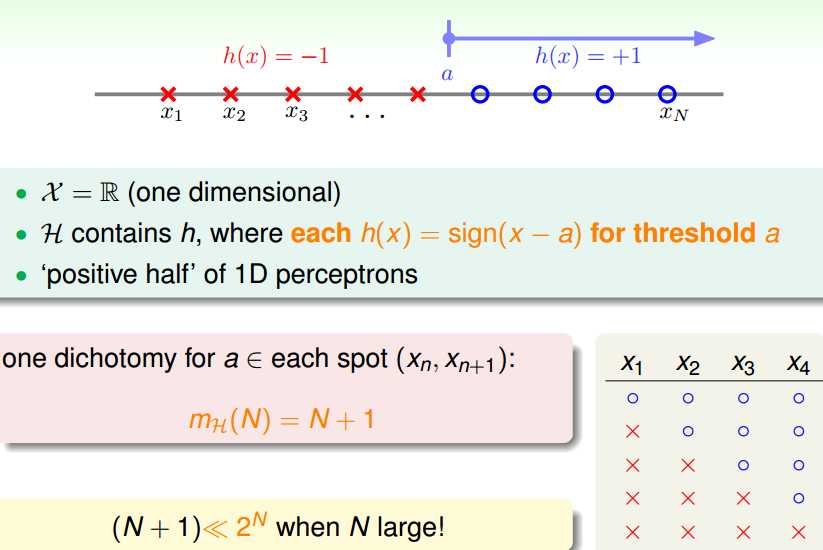

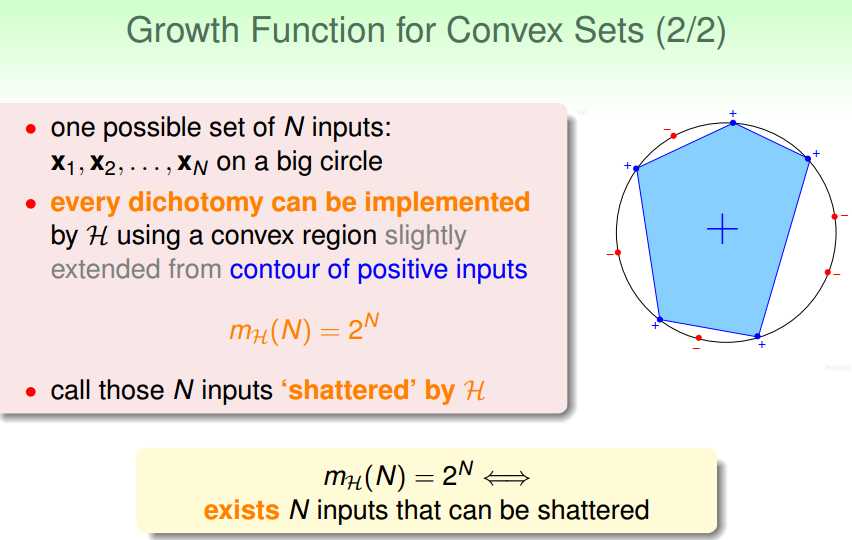
集合可自由选择的Hoeffding不等式和上述增长函数,我们得到


断点和mh的数量级之间的关系:

标签:cti eth 不同 技术 nbsp 上界 等于 point 分享
原文地址:http://www.cnblogs.com/futurehau/p/6246784.html