标签:进一步 ges 逆矩阵 等于 多次 att .com 输入 最大
前面一节我们通过引入增长函数的上限的上限,一个多项式,来把Ein 和 Eout 的差Bound住,这一节引入VC Bound进一步说明这个问题。
前边我们得到,如果一个hypethesis集是有break point的,那么最终mh会被一个多项式bound住,如果break point 为k的话,那么这个多项式为N^(k - 1)。
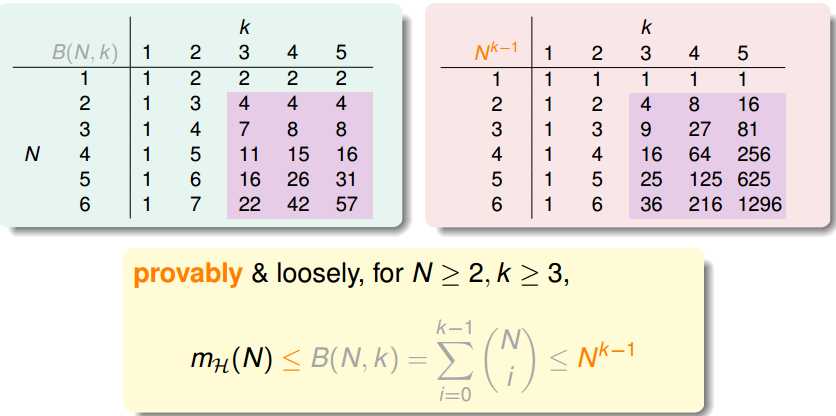
Bound的不等式这里系统的列一下就是:

也就是说,机器可以学习的即可条件:
要有好的假设集,也就是需要存在break point
训练数据集要足够的大
要有一点儿好运气,选到了一个小的Ein。
好了,接下来正式介绍VC Dimension
VC Dimension是能够shatter的最大的N,也就是最小的break point - 1
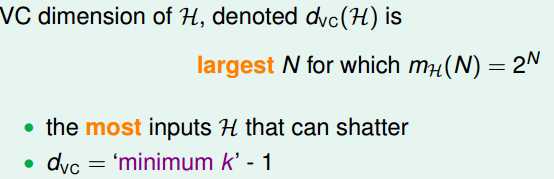

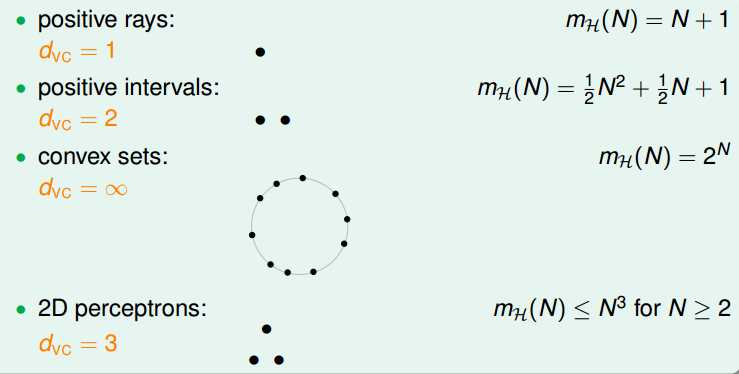
那么,之前讨论过break point的几种hypethesis对应的VC Dimension就对应为:
好了,有了VC Dimension,那么我们就可以从VC Dimension的角度来来看看我们之前的PLA,可以分为两条主线:
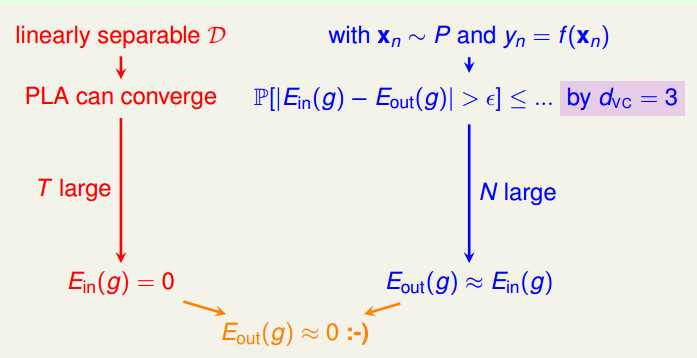
那么,接下来扩展到具有超过两个特征的PLA。

那么,猜想perception的VC Dimension是不是就是 d + 1 呢?实际上就是的,怎么证明呢?当然就是从dvc >= d + 1 和 dvc <= d + 1 两个方面来证明。
一方面,欲证 dvc >= d + 1,只需要找到某个训练集大小为d + 1,可以内shatter即可:
假设这些输入数据为:
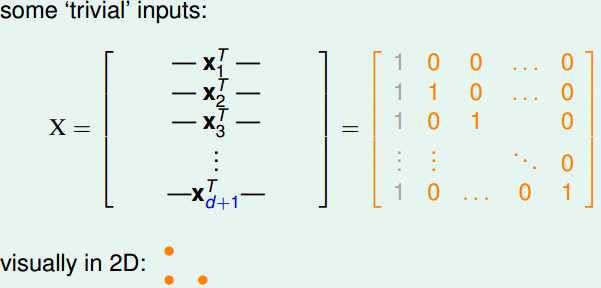
其中第一列为加进去的常数项,可以X是一个可逆矩阵
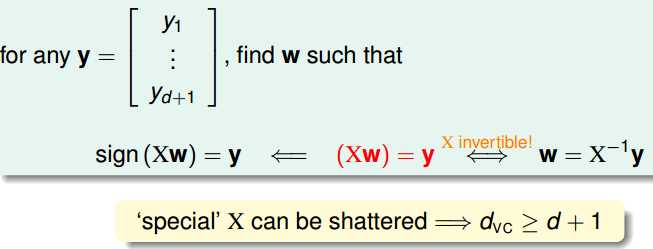
得证。
另一方面,欲证dvc <= d +1,就需要证明对所有的大小为d + 2的数据都不能shatter
特别地,对于 2 perception,输入数据如下边所示,可以得到x4 = x1 + x2 - x3,那么两边同时乘以wt可知:
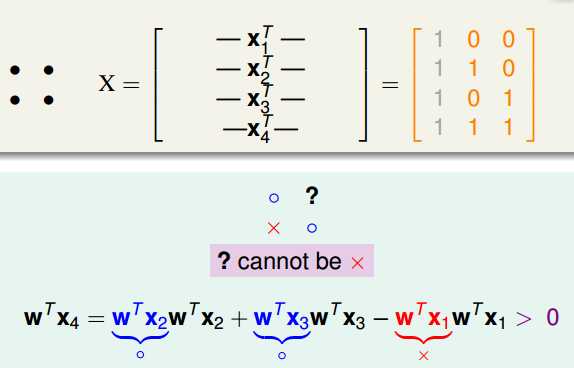
最后如果y4是负就不可以得到,也就是不能够shatter。
一般化,

X列为n + 1,行为d + 2,所以第d + 2一定可以被前边的d + 1行线性表示。
两边同乘w,然后右边取值与线性系数一样,这样导致右边都为正,
所以y(d + 2)为负不能够取得,也就是对所有的大小的d + 2的都不能shatter。

dvc 约等于 free parameters


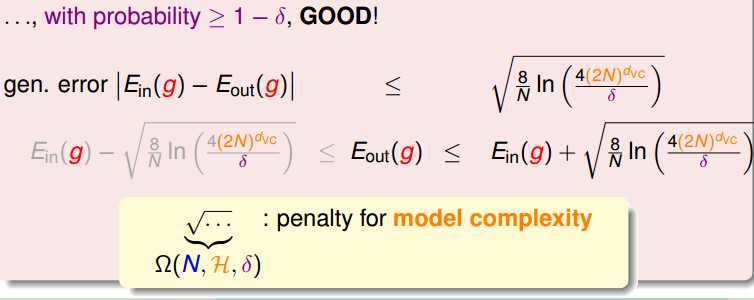
所以VC Bound透露的信息:
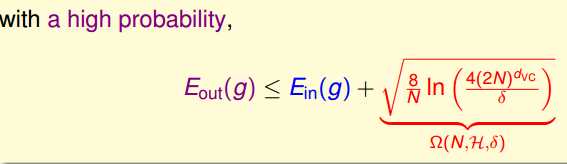

上图就更好的说明了 VC Dimension 在某种程度上代表了模型复杂度。

上图举例列举了我们需要达到某个指标时候的数据,首先理论上这些数据似乎是非常大的,
但由于我们在推导VC Bound的时候,多次进行了上界扩张,所以实际上并不需要这么大,只需要十倍的dvc就可以了。

至此,通过理解机器为什么可以学习系列文章讲清楚了这个问题。
标签:进一步 ges 逆矩阵 等于 多次 att .com 输入 最大
原文地址:http://www.cnblogs.com/futurehau/p/6260332.html