Convolution Matrix

Here is a mathematician‘s domain. Most of filters are using convolution matrix. With the Convolution Matrix filter, if the fancy takes you, you can build a custom filter.

What is a convolution matrix? It‘s possible to get a rough idea of it without using mathematical tools that only a few ones know. Convolution is the treatment of a matrix by another one which is called “kernel”.

The Convolution Matrix filter uses a first matrix which is the Image to be treated. The image is a bi-dimensional collection of pixels in rectangular coordinates. The used kernel depends on the effect you want.

GIMP uses 5x5 or 3x3 matrices. We will consider only 3x3 matrices, they are the most used and they are enough for all effects you want. If all border values of a kernel are set to zero, then system will consider it as a 3x3 matrix.

The filter studies successively every pixel of the image. For each of them, which we will call the “initial pixel”, it multiplies the value of this pixel and values of the 8 surrounding pixels by the kernel corresponding value. Then it adds the results, and the initial pixel is set to this final result value.

A simple example:     

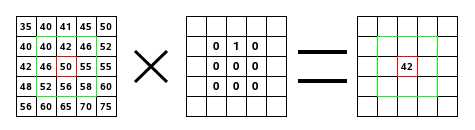
On the left is the image matrix: each pixel is marked with its value. The initial pixel has a red border. The kernel action area has a green border. In the middle is the kernel and, on the right is the convolution result.

Here is what happened: the filter read successively, from left to right and from top to bottom, all the pixels of the kernel action area. It multiplied the value of each of them by the kernel corresponding value and added results. The initial pixel has become 42: (40*0)+(42*1)+(46*0) + (46*0)+(50*0)+(55*0) + (52*0)+(56*0)+(58*0) = 42. (the filter doesn‘t work on the image but on a copy). As a graphical result, the initial pixel moved a pixel downwards.