标签：0.11 简单 logs 类型 python div 计算 blog 多个
奇异值分解（Singular Value Decompositon,SVD），可以实现用小得多的数据集来表示原始数据集。
优点：简化数据，取出噪声，提高算法的结果
缺点：数据的转换可能难以理解
适用数据类型：数值型数据
SVD最早的应用之一是信息检索，我们称利用SVD的方法为隐形语义索引（LSI）或者隐形语义分析（LSA）。
在LSI中，一个矩阵是有文档和词语组成的。当我们在该矩阵上应用SVD的时候，就会构建出多个奇异值。这些奇异值代表了文档中的概念或者主题，这一特点可以用于更高效的文档检索。
SVD的另一个应用就是推荐系统。简单版本的推荐系统能够计算项或者人之间的相似度。更先进的方法则先利用SVD从数据中构建一个主题空间，然后再在该空间下计算其相似度。
SVD将原始的数据集矩阵Data分解成三个矩阵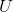 
、
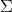和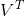 
。
如果数据集矩阵Data是M×N的，那么 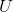是M×M的、 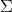是M×N的、 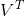是N×N的。
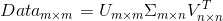
矩阵 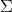中只有从大到小排列的对角元素。在某个奇异值的数目（r个）之后，其他的奇异值都置为0，这就意味这数据集中仅有r个重要特征，而其余特征则都是噪声或者冗余特征。
利用Python实现SVD
>> X=[0.3619 0.2997 0.1331 0.3296;0.1695 0.3628 0.0817 0.2826;0.1159 0.5581 0.0828 0.3718;0.1508 0.1077 0.0539 0.1274] #Matlab
X =
0.3619 0.2997 0.1331 0.3296
0.1695 0.3628 0.0817 0.2826
0.1159 0.5581 0.0828 0.3718
0.1508 0.1077 0.0539 0.1274
>> [U,S,V] = svd (X) #Matlab
U =
-0.5468 0.6999 0.1302 -0.4406
-0.4846 -0.0839 0.5883 0.6420
-0.6496 -0.6312 -0.3105 -0.2883
-0.2102 0.3234 -0.7352 0.5574
S =
1.0245 0 0 0
0 0.2608 0 0
0 0 0.0001 0
0 0 0 0.0000
V =
-0.3778 0.8233 -0.4206 -0.0508
-0.7076 -0.5297 -0.3661 -0.2911
-0.1733 0.1974 0.6302 -0.7307
-0.5715 0.0518 0.5403 0.615
标签：0.11 简单 logs 类型 python div 计算 blog 多个
原文地址：http://www.cnblogs.com/tonglin0325/p/6307254.html
