标签:集合 http com 优秀 问题 strong 元素 .com log
被大神hzm鄙视了一番,我便觉得这个带花树非学不可啦!!话不多说,下面就是我的学习随笔!
带花树算法就是用来解决一般图的匹配问题。一般图匹配自然是比二分图匹配高级的东西!所以立马屁颠屁颠地去复习了匈牙利算法。这两个算法的核心思想都是“增广”!既然这样,我们就通过对匈牙利算法增广概念的复习来引入带花树算法的增广从而理解带花树算法吧!!_(:зゝ∠)_
匈牙利算法的增广路
咳咳,我们来复习一下二分图匹配的问题吧!已知集合S和集合T以及若干S集合中的元素到T集合中的元素的二元关系(s,t)。选出若干(s‘,t‘)的关系满足,s‘的集合S‘,t‘的集合T‘,其自身元素不重复。现在求解选出最多的(s , t)二元关系的方案。很明显,每选一条边(s,t),会影响所有直接间接与s或t相连的边的选取方案。增广路的思想就是说:对于一种方案,从一个未选点出发,如果能经过【未选边】->【已选边】->【未选边】->......->【已选边】->【未选边】如是的一条路径,则称这样的路径为增广路;那么,这是我们有n个已选边,n+1个未选边,那么将已选未选边交换一下状态,就得到了路径上n+1个已选边,n个未选边的更优秀的解。而且我们可以证明找不到增广路时,就没有更优秀的解了。所以只要不停增广,一直到增广不了就可以解决这个问题了!
带花树算法的增广路
如果我们把增广路的概念拓展到一般图行不行呢。当然行啊!但是有一点不妥的就是一般图有环,而且可能有奇(ji)环。所以我们的处理肯定会有不同的地方。
先考虑一致的地方吧!同样,我们每次可以选取一个没有和其他点匹配的点,然后BFS一直走到最近的没有选取的点,这就是一条增广路,然后翻转路径上的已选点未选点关系:如下图
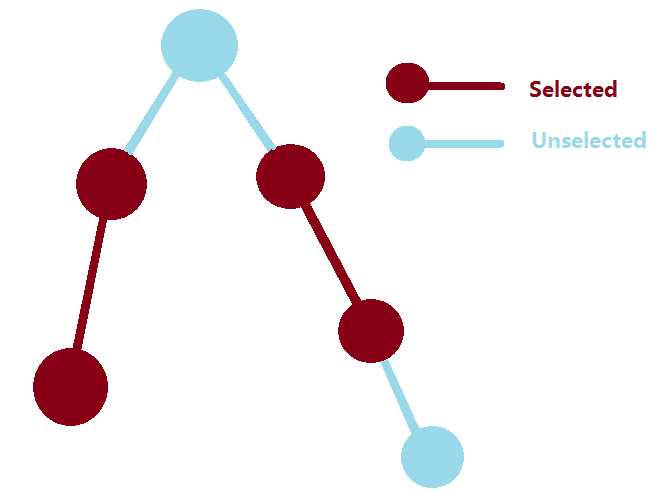

那有环怎么办呢
标签:集合 http com 优秀 问题 strong 元素 .com log
原文地址:http://www.cnblogs.com/JeffLee-AuB/p/6336660.html