标签:[1] void com 技术分享 中国 gif cin 关联 xrange
这两题原理是一样的,不过第二题数据量大一些。这个累加操作相当于一个矩阵乘法,然后用矩阵中的第一列数和输入的数组做卷积,比如这个样例处理2次矩阵就是这样的
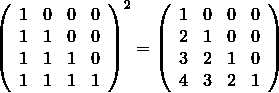
然后取出第一列数和输入的数做卷积,也就是多项式乘法
$\left(1+2x+3x^2+4x^3\right) \left(1+3x+5x^2+6x^3\right)=1 + 5 x + 14 x^2 + 29 x^3 + 39 x^4 + 38 x^5 + 24 x^6$
前四项的系数1,5,14,29就是结果了
这第一列数我们可以不用矩阵乘法做,经过观察发现它们是一些有关联的组合数,而且可以递推O(n)求出第一列数
$C_0=1,C_i=\frac{C_{i-1} (i+k-1)}{i}$
除法用逆元处理,第一题数据量小用O(n^2)模拟乘法就行了,Python写的

1 n,k=map(int,raw_input().split()) 2 c=[1]*n 3 p=10**9+7 4 a=[int(input()) for i in xrange(n)] 5 inv=[1]*5005 6 for i in range(2,5005): 7 inv[i] =(p-p//i) * inv[p%i] % p 8 for i in xrange(1,n): 9 c[i]=c[i-1]*(k-1+i)*inv[i]%p 10 c.reverse() 11 for i in xrange(1,n+1): 12 s=0 13 for j in xrange(i): 14 s=s+a[j]*c[-(i-j)] 15 print(s%p)
第二题50000数据就需要FFT了,还需要模1e9+7,我们用数论变换+中国剩余定理做

1 #include <iostream> 2 using namespace std; 3 4 #define N 340030 5 #define M 340020 6 #define LL long long 7 #define mod 1000000007 8 #define K 3 9 10 const int m[K] = {1004535809, 998244353, 104857601}; 11 const int G = 3; 12 13 LL qpow(LL x, LL k, LL p) { 14 int ret = 1; 15 while(k) { 16 if(k & 1) ret = 1LL * ret%p * x % p; 17 k >>= 1; 18 x = 1LL * x%p * x % p; 19 } 20 return ret; 21 } 22 struct _NTT { 23 LL wn[25], p; 24 25 void init(LL _p) { 26 p = _p; 27 for(int i = 1; i <= 21; ++i) { 28 int t = 1 << i; 29 wn[i] = qpow(G, (p - 1) / t, p); 30 } 31 } 32 void change(LL *y, int len) { 33 for(int i = 1, j = len / 2; i < len - 1; ++i) { 34 if(i < j) swap(y[i], y[j]); 35 int k = len / 2; 36 while(j >= k) j -= k, k /= 2; 37 j += k; 38 } 39 } 40 void NTT(LL y[], int len, int on) { 41 change(y, len); 42 int id = 0; 43 for(int h = 2; h <= len; h <<= 1) { 44 ++id; 45 for(int j = 0; j < len; j += h) { 46 LL w = 1; 47 for(int k = j; k < j + h / 2; ++k) { 48 int u = y[k]; 49 int t = y[k+h/2] * w % p; 50 y[k] = u + t; 51 if(y[k] >= p) y[k] -= p; 52 y[k+h/2] = u + p - t; 53 if(y[k+h/2] >= p) y[k+h/2] -= p; 54 w = w * wn[id] % p; 55 } 56 } 57 } 58 if(on == -1) { 59 for(int i = 1; i < len / 2; ++i) swap(y[i], y[len-i]); 60 int inv = qpow(len, p - 2, p); 61 for(int i = 0; i < len; ++i) 62 y[i] = 1LL * y[i] * inv % p; 63 } 64 } 65 void mul(LL A[], LL B[], LL len) { 66 NTT(A, len, 1); 67 NTT(B, len, 1); 68 for(int i = 0; i < len; ++i) A[i] = 1LL * A[i] * B[i] % p; 69 NTT(A, len, -1); 70 } 71 }ntt[K]; 72 73 LL tmp[N][K], t1[N], t2[N]; 74 LL x1[N], x2[N]; 75 LL r[K][K]; 76 77 LL CRT(LL a[]) { 78 LL x[K]; 79 for(int i = 0; i < K; ++i) { 80 x[i] = a[i]; 81 for(int j = 0; j < i; ++j) { 82 int t = (x[i] - x[j]) % m[i]; 83 if(t < 0) t += m[i]; 84 x[i] = 1LL * t * r[j][i] % m[i]; 85 } 86 } 87 LL mul = 1, ret = x[0] % mod; 88 for(int i = 1; i < K; ++i) { 89 mul = 1LL * mul * m[i-1] % mod; 90 ret += 1LL * x[i] * mul % mod; 91 if(ret >= mod) ret -= mod; 92 } 93 return ret; 94 } 95 96 void mul(LL A[], LL B[], LL len) { 97 for(int id = 0; id < K; ++id) { 98 for(int i = 0; i < len; ++i) { 99 t1[i] = A[i], t2[i] = B[i]; 100 } 101 ntt[id].mul(t1, t2, len); 102 for(int i = 0; i < len; ++i) { 103 tmp[i][id] = t1[i]; 104 } 105 } 106 for(int i = 0; i < len; ++i) A[i] = CRT(tmp[i]); 107 } 108 109 LL a[N],b[N]; 110 LL inv[50005]; 111 112 void init() { 113 for(int i = 0; i < K; ++i) { 114 for(int j = 0; j < i; ++j) 115 r[j][i] = qpow(m[j], m[i] - 2, m[i]); 116 } 117 for(int i = 0; i < K; ++i) ntt[i].init(m[i]);//ntt的初始化到这里结束 118 inv[1]=1; 119 for(int x=2;x<50003;x++)inv[x]=(mod-mod/x)*inv[mod%x]%mod; 120 } 121 122 123 int main() 124 { 125 init(); 126 int n,k,i; 127 cin>>n>>k; 128 b[0]=1; 129 for(i=1;i<n;i++) 130 { 131 b[i]=b[i-1]*(k-1+i)%mod*inv[i]%mod;//求矩阵第一列系数 132 b[i]=(b[i]+mod)%mod; 133 } 134 for(i=0;i<n;i++) 135 { 136 cin>>a[i]; 137 } 138 mul(a,b,1<<17);//做卷积 139 for(i=0;i<n;i++) 140 { 141 cout<<(a[i]+mod)%mod<<endl; 142 } 143 return 0; 144 }
51nod 1161 Partial Sums,1172 Partial Sums V2
标签:[1] void com 技术分享 中国 gif cin 关联 xrange
原文地址:http://www.cnblogs.com/czp001/p/6340012.html