标签:learning 公式 函数 二维 实际应用 数据分布 简单 mat des
相比于week1中讨论的单变量的线性回归,多元线性回归更具有一般性,应用范围也更大,更贴近实际。
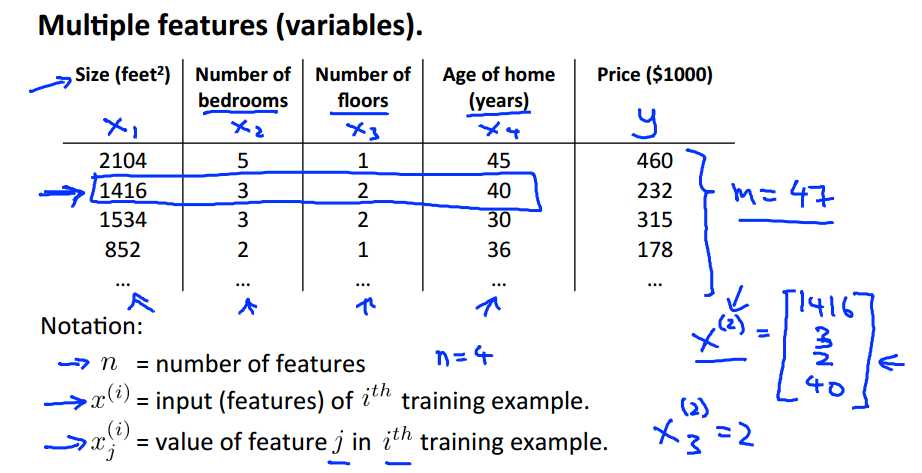
上面就是接上次的例子,将房价预测问题进行扩充,添加多个特征(features),使问题变成多元线性回归问题。
多元线性回归将通过更多的输入特征,来预测输出。上面有新的Notation(标记)需要掌握。
相比于之前的假设:![]()
我们将多元线性回归的假设修改为:
![]()
每一个xi代表一个特征;为了表达方便,令x0=1,可以得到假设的矩阵形式:

其中,x和theta分别表示:
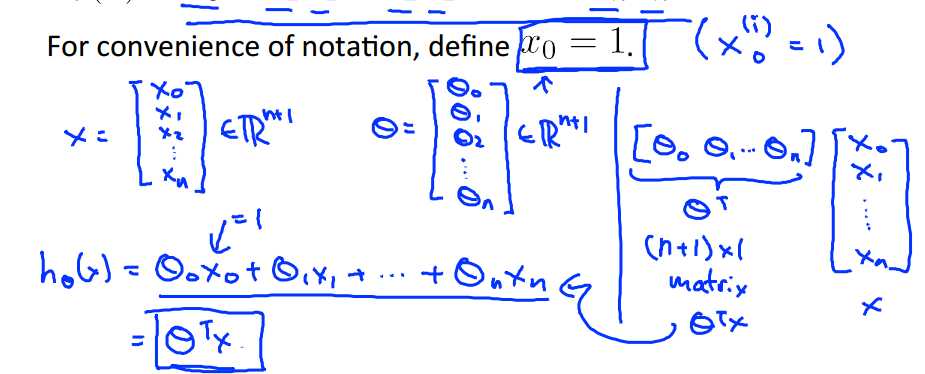
所有的训练样本按行存贮在矩阵X中,看一个例子:
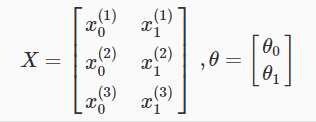
这样,我们可以通过向量的计算,直接得到一个m×1的假设结果向量:![]()
梯度下降的通用形式依然不会变化:
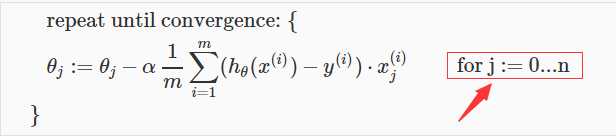
只是,和单变量线性回归不同的是,多元线性回归需要同时迭代n+1个theta;

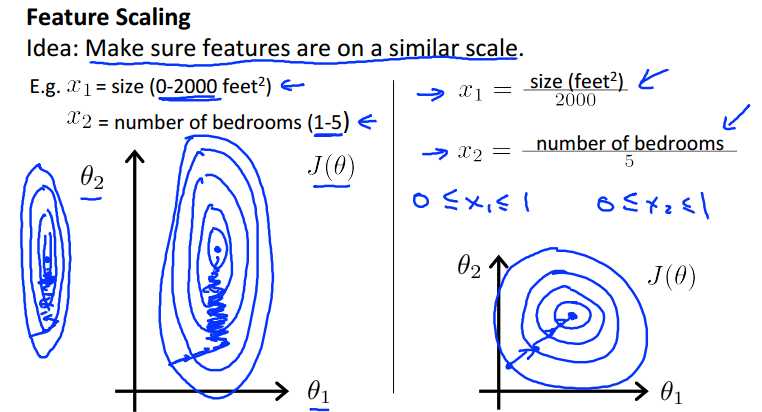
特征归一化,总的说来是为了让特征之间的数值差距缩小,使数据分散在同一个数量级范围。
关于这样做的好处,可以减小数量级偏大的特征对数量级偏小特征的影响,比如上面所说的房屋面积size,和卧室数量;
如果将这两个特征画在上面的二维图中,就会变成一个瘦长的椭圆。
总之,如果想要使梯度下降算法收敛的更快,就需要使用特征归一化Feature Scaling,使特征分布在相近的范围中。
使新的特征最好分布在[-1,1]中,如上面使用xi/(数据范围:max-min)。
通常情况下,数据分布在[-1/3,1/3] or [-3,3]都是可以接受的。

正规化均值,使数据集的均值为0.(不要对x0使用)
可以一步同时完成数据归一和正规化:
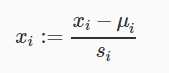
其中μi为对应特征的均值;Si是特征数据已知的分布范围,通常是(max - min)来计算,或者为数据的标准差。
学习率a对于梯度下降是关键,下面就来讨论如何选取使算法高效运行的a值。

我们可以作关于损失函数 J(theta)和 迭代次数的函数,在指定的学习率a下的图象,
如果函数 J 不是单调减小的,那么需要减小a。
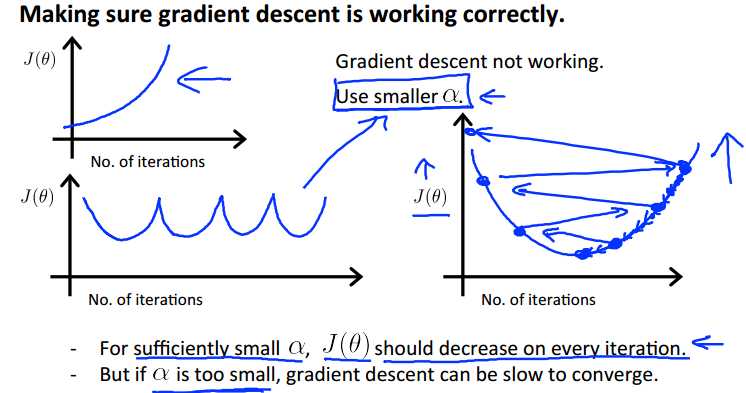
多次选择a,需要得到一个足够小的a,使得 J 在每一步迭代中都 不断减小;
但是如果a太小,梯度下降会收敛的很慢,这时也需要略微增大a。
选择a的原则:最好先找到最大的使 J 单调减小的a,最终选择比最大的a略小的值。
每次选择可以增大或减小3倍,然后再增大或减小数量级。

实际应用中,我们只使用简单的‘直线’回归显然是不够的,我们大多数情况下需要使用多项式拟合。
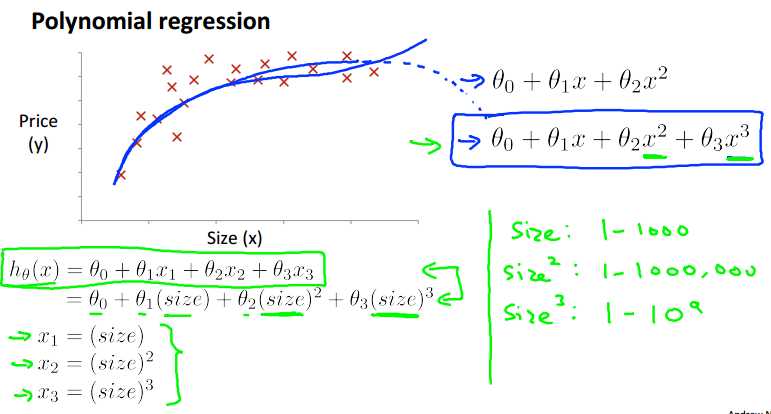
单看这些数据点的分布,直观上感觉使用曲线比直线拟合的效果要好一些。
根据实际的例子,关于房价的预测,size越大,房价不会下跌,选用三次函数拟合数据更好。
同时,平方根函数也是不错的选择:![]() 。
。
(注:如使用多项式回归,一定要使用特征归一化)
Normal Equation是另外一种求参数theta的方法。
我们知道,梯度下降反复迭代的目的,就是求得那个最优解,而Normal Equation的思想就是直接通过求导,得到theta。
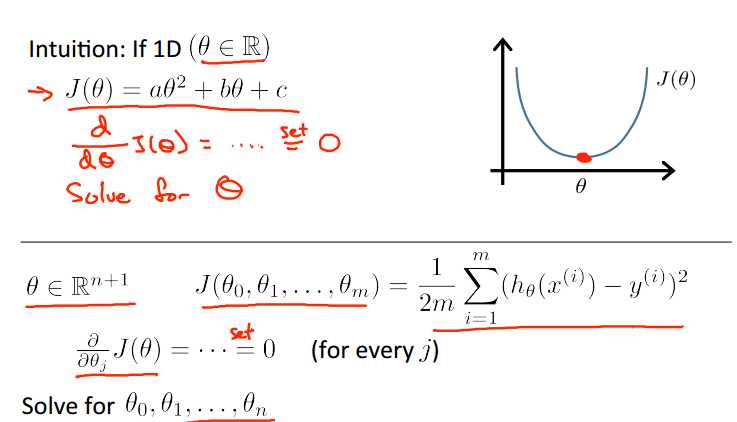
其对所有的θj分别求偏导数,然后使它们为0,解这些方程组,求得theta。
这样就不需要通过反复迭代而直接求得结果,效率颇高。下面是一个例子:
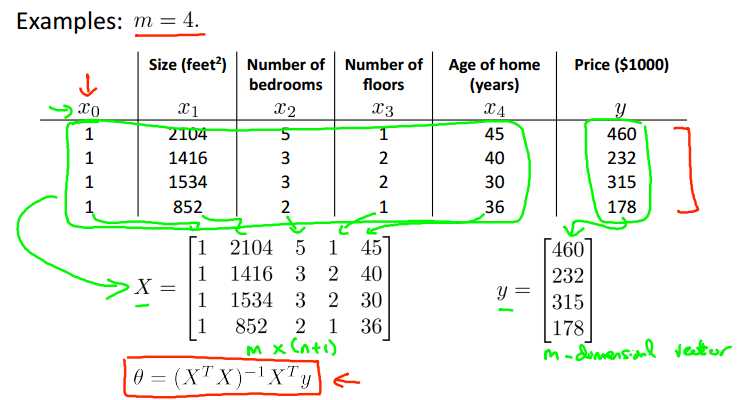
这是方法的矩阵表示:
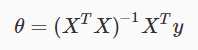
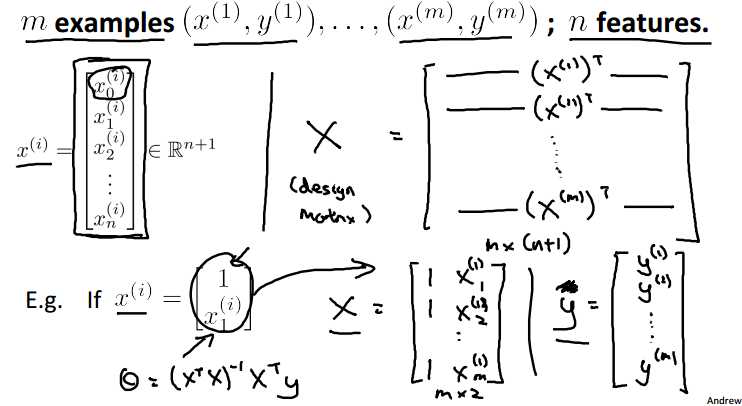

相较于梯度下降,Normal Equation有以下优势:
不需要选择a,不需要进行迭代,只需计算一个n×n的转置矩阵,算法效率高,
而且在Normal Equation中不需要进行特征归一化操作。
注意:当n>10,000时,Normal Equation的计算代价过大,建议使用梯度下降。

如果XTX不可逆,根据上面的Normal Equation求theta的公式,原则上是不能使用的,那应该怎么处理这种情况?
XTX不可逆的情况:
1)冗余的特征(呈线性关系):删除多余的特征;
2)特征过多,训练数据过少(m<=n):删除某些特征,或 使用“regularization ”。
斯坦福机器学习视频笔记 Week2 Linear Regression with Multiple Variables
标签:learning 公式 函数 二维 实际应用 数据分布 简单 mat des
原文地址:http://www.cnblogs.com/yangmang/p/6347869.html