标签:合并 分析 csdn 技术分享 logs article ted 表示 tail
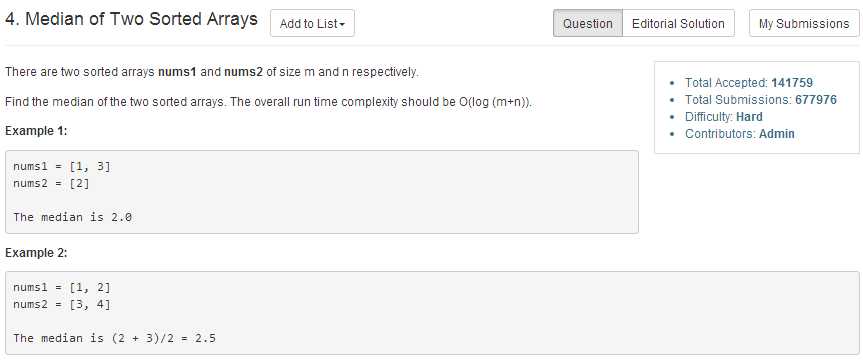
本题我最开始的思路是,将两数组合并后排序,找出中位数返回。不过很明显是超时的。
下面是我在http://blog.csdn.net/yutianzuijin/article/details/11499917看到的思路:
首先假设数组A和B的元素个数都大于k/2,我们比较A[k/2-1]和B[k/2-1]两个元素,这两个元素分别表示A的第k/2小的元素和B的第k/2小的元素。这两个元素比较共有三种情况:>、<和=。如果A[k/2-1]<B[k/2-1],这表示A[0]到A[k/2-1]的元素都在A和B合并之后的前k小的元素中。换句话说,A[k/2-1]不可能大于两数组合并之后的第k小值,所以我们可以将其抛弃。
当A[k/2-1]>B[k/2-1]时存在类似的结论。
当A[k/2-1]=B[k/2-1]时,我们已经找到了第k小的数,也即这个相等的元素,我们将其记为m。由于在A和B中分别有k/2-1个元素小于m,所以m即是第k小的数。(这里可能有人会有疑问,如果k为奇数,则m不是中位数。这里是进行了理想化考虑,在实际代码中略有不同,是先求k/2,然后利用k-k/2获得另一个数。)
通过上面的分析,我们即可以采用递归的方式实现寻找第k小的数。此外我们还需要考虑几个边界条件:
1 double findKth(int a[], int m, int b[], int n, int k) 2 { 3 //always assume that m is equal or smaller than n 4 if (m > n) 5 return findKth(b, n, a, m, k); 6 if (m == 0) 7 return b[k - 1]; 8 if (k == 1) 9 return min(a[0], b[0]); 10 //divide k into two parts 11 int pa = min(k / 2, m), pb = k - pa; 12 if (a[pa - 1] < b[pb - 1]) 13 return findKth(a + pa, m - pa, b, n, k - pa); 14 else if (a[pa - 1] > b[pb - 1]) 15 return findKth(a, m, b + pb, n - pb, k - pb); 16 else 17 return a[pa - 1]; 18 } 19 20 class Solution 21 { 22 public: 23 double findMedianSortedArrays(int A[], int m, int B[], int n) 24 { 25 int total = m + n; 26 if (total & 0x1) 27 return findKth(A, m, B, n, total / 2 + 1); 28 else 29 return (findKth(A, m, B, n, total / 2) 30 + findKth(A, m, B, n, total / 2 + 1)) / 2; 31 } 32 };
标签:合并 分析 csdn 技术分享 logs article ted 表示 tail
原文地址:http://www.cnblogs.com/lca1826/p/6359836.html