标签:uniq elf head namespace 向量 represent names 二维 strong
地址:
题目:
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 4295 | Accepted: 2697 |
Description
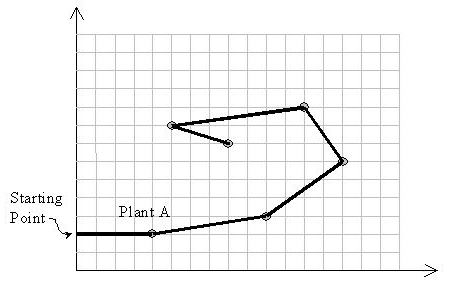
Input
Output
Sample Input
2 10 1 4 5 2 9 8 3 5 9 4 1 7 5 3 2 6 6 3 7 10 10 8 8 1 9 2 4 10 7 6 14 1 6 11 2 11 9 3 8 7 4 12 8 5 9 20 6 3 2 7 1 6 8 2 13 9 15 1 10 14 17 11 13 19 12 5 18 13 7 3 14 10 16
Sample Output
10 8 7 3 4 9 5 6 2 1 10 14 9 10 11 5 12 8 7 6 13 4 14 1 3 2
思路:直接用卷包裹法求凸包即可
代码:
1 /* 二维几何 */ 2 /* 需要包含的头文件 */ 3 #include <cstdio> 4 #include <cmath > 5 #include <iostream> 6 #include <algorithm> 7 #include <cstring> 8 #include <map> 9 using namespace std; 10 /** 常用的常量定义 **/ 11 const double INF = 1e200; 12 const double eps = 1e-10; 13 const double PI = acos(-1.0); 14 const int Max = 100; 15 /** 基本几何结构 **/ 16 struct Point 17 { 18 double x,y; 19 Point(double a=0, double b=0){x=a,y=b;} 20 bool operator<(const Point &ta)const 21 { 22 if(x==ta.x) return y<ta.y; 23 return x<ta.x; 24 } 25 friend Point operator+(const Point &ta,const Point &tb) 26 { 27 return Point(ta.x+tb.x,ta.y+tb.y); 28 } 29 friend Point operator-(const Point &ta,const Point &tb) 30 { 31 return Point(ta.x-tb.x,ta.y-tb.y); 32 } 33 }; 34 struct Vec2D //二维向量,*重载为点乘,/重载为叉乘 35 { 36 double x,y; 37 Vec2D(double ta,double tb){x=ta,y=tb;} 38 Vec2D(Point &ta){x=ta.x,y=ta.y;} 39 friend double operator*(const Vec2D &ta,const Vec2D &tb) 40 { 41 return ta.x*tb.x+ta.y*tb.y; 42 } 43 friend double operator/(const Vec2D &ta,const Vec2D &tb) 44 { 45 return ta.x*tb.y-ta.y*tb.x; 46 } 47 friend Vec2D operator+(const Vec2D &ta,const Vec2D &tb) 48 { 49 return Vec2D(ta.x+tb.x,ta.y+tb.y); 50 } 51 friend Vec2D operator-(const Vec2D &ta,const Vec2D &tb) 52 { 53 return Vec2D(ta.x-tb.x,ta.y-tb.y); 54 } 55 Vec2D operator=(const Vec2D &ta) 56 { 57 x=ta.x,y=ta.y; 58 return *this; 59 } 60 }; 61 struct LineSeg //线段,重载了/作为叉乘运算符,*作为点乘运算符 62 { 63 Point s,e; 64 LineSeg(){s=Point(0,0),e=Point(0,0);} 65 LineSeg(Point a, Point b){s=a,e=b;} 66 double lenth(void) 67 { 68 return sqrt((s.x-e.x)*(s.x-e.x)+(s.y-e.y)*(s.y-e.y)); 69 } 70 friend double operator*(const LineSeg &ta,const LineSeg &tb) 71 { 72 return (ta.e.x-ta.s.x)*(tb.e.x-tb.s.x)+(ta.e.y-ta.s.y)*(tb.e.y-tb.s.y); 73 } 74 friend double operator/(const LineSeg &ta,const LineSeg &tb) 75 { 76 return (ta.e.x-ta.s.x)*(tb.e.y-tb.s.y)-(ta.e.y-ta.s.y)*(tb.e.x-tb.s.x); 77 } 78 LineSeg operator=(const LineSeg &ta) 79 { 80 s=ta.s,e=ta.e; 81 return *this; 82 } 83 }; 84 struct Line // 直线的解析方程 a*x+b*y+c=0 为统一表示,约定 a >= 0 85 { 86 double a,b,c; 87 Line(double d1=1, double d2=-1, double d3=0){ a=d1,b=d2,c=d3;} 88 }; 89 90 double getdis(Point &ta,Point &tb) 91 { 92 return sqrt((ta.x-ta.x)*(ta.x-tb.x)+(ta.y-tb.y)*(ta.y-tb.y)); 93 } 94 /** ************凸包graham算法**************** 95 寻找凸包的graham 扫描法 96 PS(PointSet)为输入的点集; 97 tb为输出的凸包上的点集,按照逆时针方向排列; 98 n为PointSet中的点的数目 99 num为输出的凸包上的点的个数 100 ****************************************** **/ 101 bool cmp(const Point &ta,const Point &tb)// 选取与最后一条确定边夹角最小的点,即余弦值最大者 102 { 103 // double tmp=LineSeg(ps[0],ta)/LineSeg(ps[0],tb); 104 // if(fabs(tmp)<eps) 105 // return getdis(ps[0],ta)<getdis(ps[0],tb); 106 // else if(tmp>0) 107 // return 1; 108 return 0; 109 } 110 void graham(Point ps[],Point tb[],int n,int &num) 111 { 112 int cur=0,top=2; 113 for(int i=1;i<n;i++) 114 if(ps[cur].y>ps[i].y || (ps[cur].y==ps[i].y &&ps[cur].x>ps[i].x)) 115 cur=i; 116 swap(ps[cur],ps[0]); 117 sort(ps+1,ps+n,cmp); 118 tb[0]=ps[0],tb[1]=ps[1],tb[2]=ps[2]; 119 for(int i=3;i<n;i++) 120 { 121 while(LineSeg(tb[top-1],tb[top])/LineSeg(tb[top-1],ps[i])<0) 122 top--; 123 tb[++top]=ps[i]; 124 } 125 num=top+1; 126 } 127 /** 卷包裹法求点集凸壳,参数说明同graham算法 **/ 128 void ConvexClosure(Point ps[],Point tb[],int n,int &num) 129 { 130 LineSeg lx,ly; 131 int cur; 132 bool vis[Max]; 133 num=-1,cur=0; 134 memset(vis,0,sizeof(vis)); 135 for(int i=1;i<n;i++) 136 if(ps[cur].y>ps[i].y || (ps[cur].y==ps[i].y &&ps[cur].x>ps[i].x)) 137 cur=i; 138 tb[++num]=ps[cur]; 139 lx.s=Point(ps[cur].x-1,ps[cur].y),lx.e=ps[cur]; 140 vis[cur]=1; 141 // 选取与最后一条确定边夹角最小的点,即余弦值最大者 142 while(num!=n) 143 { 144 int ch; 145 double mxcross=-2,midis,tmxcross; 146 ly.s=lx.e; 147 for(int i=0;i<n;i++)if(!vis[i]) 148 { 149 ly.e=ps[i]; 150 tmxcross=(lx*ly)/lx.lenth()/ly.lenth(); 151 if(tmxcross>mxcross ||(fabs(tmxcross-mxcross)<eps && getdis(ly.s,ly.e)<midis)) 152 mxcross=tmxcross,midis=getdis(ly.s,ly.e),ch=i; 153 } 154 tb[++num]=ps[ch],vis[ch]=1; 155 lx.s=tb[num-1],lx.e=tb[num],ly.s=tb[num]; 156 } 157 } 158 159 map<Point,int>mp; 160 Point ps[Max],tb[Max]; 161 int main(void) 162 { 163 int t;cin>>t; 164 while(t--) 165 { 166 mp.clear(); 167 int n,ans;cin>>n; 168 for(int i=0,id,x,y;i<n;i++) 169 scanf("%d%d%d",&id,&x,&y),ps[i]=Point(x,y),mp[ps[i]]=id; 170 ConvexClosure(ps,tb,n,ans); 171 printf("%d ",ans); 172 for(int i=0;i<ans;i++) 173 printf("%d%c",mp[tb[i]],i==ans-1?‘\n‘:‘ ‘); 174 } 175 return 0; 176 }
标签:uniq elf head namespace 向量 represent names 二维 strong
原文地址:http://www.cnblogs.com/weeping/p/6361138.html