标签:image 分享 eal 0ms mat section arm operator 表示
地址:http://poj.org/problem?id=2826
题目:
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 13016 | Accepted: 2003 |
Description
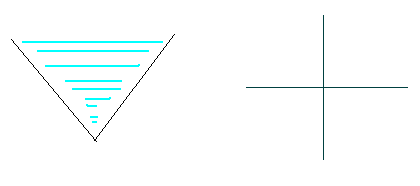
Input
Output
Sample Input
2
0 1 1 0
1 0 2 1
0 1 2 1
1 0 1 2
Sample Output
1.00 0.00
思路: 这题想还是好想,考虑到以下几种情况就可以啦。
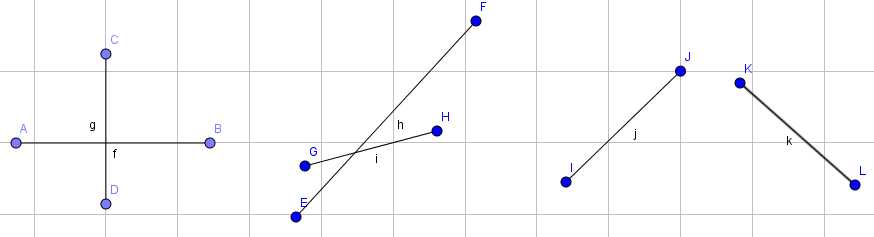
不过这傻逼题我还是玩了一天,把discuss里的所有数据都a了后还是wa!!!
因为求交点的模板错了!!!亏我还是从百度搜索求交点的页面的第一个网站上抄的模板!!!(坑人百度!!!)
还好机智的我在wa了一天后发现模板有问题,换了就ac了。
计算几何模板很重要!!!!!!!!!!!!
很重要!!!!!!!!
重要!!!!!!
因为一直wa的不能自理,所以写了两种思路的ac代码(其实差不多0.0)
1 /* 二维几何 */
2 /* 需要包含的头文件 */
3 #include <cstdio>
4 #include <cstring>
5 #include <cmath >
6 #include <iostream>
7 #include <algorithm>
8
9 using namespace std;
10 /** 常用的常量定义 **/
11 const double INF = 1e200;
12 const double eps = 1e-6;
13 const double PI = acos(-1.0);
14 const int Max = 1e6;
15
16 /** 基本几何结构 **/
17 struct Point
18 {
19 double x,y;
20 Point(double a=0, double b=0){x=a,y=b;}
21 bool operator<(const Point &ta)const
22 {
23 if(x==ta.x) return y<ta.y;
24 return x<ta.x;
25 }
26 friend Point operator+(const Point &ta,const Point &tb)
27 {
28 return Point(ta.x+tb.x,ta.y+tb.y);
29 }
30 friend Point operator-(const Point &ta,const Point &tb)
31 {
32 return Point(ta.x-tb.x,ta.y-tb.y);
33 }
34 };
35 struct Vec2D ///二维向量,*重载为点乘,/重载为叉乘
36 {
37 double x,y;
38 Vec2D(double ta,double tb){x=ta,y=tb;}
39 Vec2D(Point &ta){x=ta.x,y=ta.y;}
40 friend double operator*(const Vec2D &ta,const Vec2D &tb)
41 {
42 return ta.x*tb.x+ta.y*tb.y;
43 }
44 friend double operator/(const Vec2D &ta,const Vec2D &tb)
45 {
46 return ta.x*tb.y-ta.y*tb.x;
47 }
48 friend Vec2D operator+(const Vec2D &ta,const Vec2D &tb)
49 {
50 return Vec2D(ta.x+tb.x,ta.y+tb.y);
51 }
52 friend Vec2D operator-(const Vec2D &ta,const Vec2D &tb)
53 {
54 return Vec2D(ta.x-tb.x,ta.y-tb.y);
55 }
56 Vec2D operator=(const Vec2D &ta)
57 {
58 x=ta.x,y=ta.y;
59 return *this;
60 }
61 };
62 struct LineSeg ///线段,重载了/作为叉乘运算符,*作为点乘运算符
63 {
64 Point s,e;
65 LineSeg(){s=Point(0,0),e=Point(0,0);}
66 LineSeg(Point a, Point b){s=a,e=b;}
67 double lenth(void)
68 {
69 return sqrt((s.x-e.x)*(s.x-e.x)+(s.y-e.y)*(s.y-e.y));
70 }
71 friend double operator*(const LineSeg &ta,const LineSeg &tb)
72 {
73 return (ta.e.x-ta.s.x)*(tb.e.x-tb.s.x)+(ta.e.y-ta.s.y)*(tb.e.y-tb.s.y);
74 }
75 friend double operator/(const LineSeg &ta,const LineSeg &tb)
76 {
77 return (ta.e.x-ta.s.x)*(tb.e.y-tb.s.y)-(ta.e.y-ta.s.y)*(tb.e.x-tb.s.x);
78 }
79 LineSeg operator=(const LineSeg &ta)
80 {
81 s=ta.s,e=ta.e;
82 return *this;
83 }
84 };
85 struct Line /// 直线的解析方程 a*x+b*y+c=0 为统一表示,约定 a >= 0
86 {
87 double a,b,c;
88 Line(double d1=1, double d2=-1, double d3=0){ a=d1,b=d2,c=d3;}
89 };
90
91
92 int sgn(double ta,double tb);
93 double getdis(const Point &ta,const Point &tb);
94 double fArea(Point &ta,Point &tb,Point &tc);
95 bool intersect(LineSeg &lx,LineSeg &ly);
96 bool intersection(LineSeg &lx,LineSeg &ly,Point &pt);
97 bool cmp(const Point &ta,const Point &tb);
98 void graham(Point ps[],Point tb[],int n,int &num);
99 void ConvexClosure(Point ps[],Point tb[],int n,int &num);
100
101
102
103 int main(void)
104 {
105 int n;
106 double ans;
107 Point cs1,cs2;
108 LineSeg lx,ly,lz;
109 cin>>n;
110 while(n--)
111 {
112 ans=0;
113 cin>>lx.s.x>>lx.s.y>>lx.e.x>>lx.e.y;
114 cin>>ly.s.x>>ly.s.y>>ly.e.x>>ly.e.y;
115 if(lx.s.y>lx.e.y)
116 swap(lx.s,lx.e);
117 if(ly.s.y>ly.e.y)
118 swap(ly.s,ly.e);
119 //判断两条直线斜率,是否相交,是否重合或平行
120 if(sgn(lx.s.y,lx.e.y)&&sgn(ly.s.y,ly.e.y)&&intersect(lx,ly)&&intersection(lx,ly,cs1)==1)
121 {
122 lz=LineSeg(ly.e,Point(ly.e.x,1e5));
123 if(sgn(getdis(lx.e,cs1),getdis(ly.e,cs1))>=0 && intersect(lz,lx))
124 {
125 printf("0.00\n");
126 continue;
127 }
128 lz=LineSeg(lx.e,Point(lx.e.x,1e5));
129 if(sgn(getdis(lx.e,cs1),getdis(ly.e,cs1))<0 && intersect(lz,ly))
130 {
131 printf("0.00\n");
132 continue;
133 }
134 lz=LineSeg(Point(0,0),Point(1,0));
135 if(sgn(lz*lx/lx.lenth(),lz*ly/ly.lenth())<0)
136 swap(lx,ly);
137 if(lx.e.y>=ly.e.y)
138 {
139 lz=LineSeg(ly.e,Point(lx.e.x,ly.e.y));
140 intersection(lx,lz,cs2);
141 ans=fArea(cs1,cs2,ly.e);
142 }
143 else
144 {
145 lz=LineSeg(lx.e,Point(ly.e.x,lx.e.y));
146 intersection(ly,lz,cs2);
147 ans=fArea(cs1,cs2,lx.e);
148 }
149
150 }
151 printf("%.2f\n",ans+eps);
152
153 }
154
155 return 0;
156 }
157
158
159
160
161
162 /*******判断ta与tb的大小关系*******/
163 int sgn(double ta,double tb)
164 {
165 if(fabs(ta-tb)<eps)return 0;
166 if(ta<tb) return -1;
167 return 1;
168 }
169 /*********求两点的距离*************/
170 double getdis(const Point &ta,const Point &tb)
171 {
172 return sqrt((ta.x-tb.x)*(ta.x-tb.x)+(ta.y-tb.y)*(ta.y-tb.y));
173 }
174 /************三角形面积**************************/
175 double fArea(Point &ta,Point &tb,Point &tc)
176 {
177 return fabs(LineSeg(ta,tb)/LineSeg(ta,tc)*0.5);
178 }
179
180 /*********** 判断P1P2是否和P3P4相交****************************
181 其中Pi坐标为(xi,yi),需要满足两个条件:
182 (1)快速排斥试验:
183 以P1P2为对角线的矩形S1是否和以P3P4为对角线的矩形S2相交,
184 即 min(x1,x2)<=max(x3,x4) && min(x3,x4)<=max(x1,x2)
185 && min(y1,y2)<=max(y3,y4) &&min(y3,y4)<=max(y1,y2)
186 (2)跨立试验:
187 点P1,P2必然在线段P3P4的不同侧,
188 点P3,P4必然在线段P1P2的不同侧,
189 ***************************************************************/
190 bool intersect(LineSeg &lx,LineSeg &ly)
191 {
192 return sgn(min(lx.s.x,lx.e.x),max(ly.s.x,ly.e.x))<=0
193 && sgn(min(ly.s.x,ly.e.x),max(lx.s.x,lx.e.x))<=0
194 && sgn(min(lx.s.y,lx.e.y),max(ly.s.y,ly.e.y))<=0
195 && sgn(min(ly.s.y,ly.e.y),max(lx.s.y,lx.e.y))<=0
196 && sgn((lx/LineSeg(lx.s,ly.s))*(lx/LineSeg(lx.s,ly.e)),0)<=0
197 && sgn((ly/LineSeg(ly.s,lx.s))*(ly/LineSeg(ly.s,lx.e)),0)<=0;
198 }
199 /************线段求交点**************************
200 返回-1代表直线平行,返回0代表直线重合,返回1代表线段相交
201 利用叉积求得点P分线段DC的比,
202 然后利用高中学习的定比分点坐标公式求得分点P的坐标
203 **************************************************/
204 bool intersection(LineSeg &lx,LineSeg &ly,Point &pt)
205 {
206 pt=lx.s;
207 if(sgn(lx/ly,0)==0)
208 {
209 if(sgn(LineSeg(lx.s,ly.e)/ly,0)==0)
210 return 0;//重合
211 return -1;//平行
212 }
213 double t = (LineSeg(lx.s,ly.s)/ly)/(lx/ly);
214 pt.x+=(lx.e.x-lx.s.x)*t, pt.y+=(lx.e.y-lx.s.y)*t;
215 return 1;
216 }
217 /** ************凸包算法****************
218 寻找凸包的graham 扫描法
219 PS(PointSet)为输入的点集;
220 tb为输出的凸包上的点集,按照逆时针方向排列;
221 n为PointSet中的点的数目
222 num为输出的凸包上的点的个数
223 ****************************************** **/
224 bool cmp(const Point &ta,const Point &tb)/// 选取与最后一条确定边夹角最小的点,即余弦值最大者
225 {
226 // double tmp=LineSeg(ps[0],ta)/LineSeg(ps[0],tb);
227 // if(sgn(tmp,0)==0)
228 // return getdis(ps[0],ta)<getdis(ps[0],tb);
229 // else if(tmp>0)
230 // return 1;
231 return 0;
232 }
233 void graham(Point ps[],Point tb[],int n,int &num)
234 {
235 int cur=0,top=2;
236 for(int i=1;i<n;i++)
237 if(sgn(ps[cur].y,ps[i].y)>0 || (sgn(ps[cur].y,ps[i].y)==0 && sgn(ps[cur].x,ps[i].x)>0))
238 cur=i;
239 swap(ps[cur],ps[0]);
240 sort(ps+1,ps+n,cmp);
241 tb[0]=ps[0],tb[1]=ps[1],tb[2]=ps[2];
242 for(int i=3;i<n;i++)
243 {
244 while(sgn(LineSeg(tb[top-1],tb[top])/LineSeg(tb[top-1],ps[i]),0)<0)
245 top--;
246 tb[++top]=ps[i];
247 }
248 num=top+1;
249 }
250 /** 卷包裹法求点集凸壳,参数说明同graham算法 **/
251 void ConvexClosure(Point ps[],Point tb[],int n,int &num)
252 {
253 LineSeg lx,ly;
254 int cur,ch;
255 bool vis[Max];
256 num=-1,cur=0;
257 memset(vis,0,sizeof(vis));
258 for(int i=1;i<n;i++)
259 if(sgn(ps[cur].y,ps[i].y)>0 || (sgn(ps[cur].y,ps[i].y)==0 && sgn(ps[cur].x,ps[i].x)>0))
260 cur=i;
261 tb[++num]=ps[cur];
262 lx.s=Point(ps[cur].x-1,ps[cur].y),lx.e=ps[cur];
263 /// 选取与最后一条确定边夹角最小的点,即余弦值最大者
264 while(1)
265 {
266 double mxcross=-2,midis,tmxcross;
267 ly.s=lx.e;
268 for(int i=0;i<n;i++)if(!vis[i])
269 {
270 ly.e=ps[i];
271 tmxcross=(lx*ly)/lx.lenth()/ly.lenth();
272 if(sgn(tmxcross,mxcross)>0 ||(sgn(tmxcross,mxcross)==0 && getdis(ly.s,ly.e)<midis))
273 mxcross=tmxcross,midis=getdis(ly.s,ly.e),ch=i;
274 }
275 if(ch==cur)break;
276 tb[++num]=ps[ch],vis[ch]=1;
277 lx.s=tb[num-1],lx.e=tb[num],ly.s=tb[num];
278 }
279 }
第二种:
1 /* 二维几何 */
2 /* 需要包含的头文件 */
3 #include <cstdio>
4 #include <cstring>
5 #include <cmath >
6 #include <iostream>
7 #include <algorithm>
8
9 using namespace std;
10 /** 常用的常量定义 **/
11 const double INF = 1e200;
12 const double eps = 1e-6;
13 const double PI = acos(-1.0);
14 const int Max = 1e6;
15
16 /** 基本几何结构 **/
17 struct Point
18 {
19 double x,y;
20 Point(double a=0, double b=0){x=a,y=b;}
21 bool operator<(const Point &ta)const
22 {
23 if(x==ta.x) return y<ta.y;
24 return x<ta.x;
25 }
26 friend Point operator+(const Point &ta,const Point &tb)
27 {
28 return Point(ta.x+tb.x,ta.y+tb.y);
29 }
30 friend Point operator-(const Point &ta,const Point &tb)
31 {
32 return Point(ta.x-tb.x,ta.y-tb.y);
33 }
34 };
35 struct Vec2D ///二维向量,*重载为点乘,/重载为叉乘
36 {
37 double x,y;
38 Vec2D(double ta,double tb){x=ta,y=tb;}
39 Vec2D(Point &ta){x=ta.x,y=ta.y;}
40 friend double operator*(const Vec2D &ta,const Vec2D &tb)
41 {
42 return ta.x*tb.x+ta.y*tb.y;
43 }
44 friend double operator/(const Vec2D &ta,const Vec2D &tb)
45 {
46 return ta.x*tb.y-ta.y*tb.x;
47 }
48 friend Vec2D operator+(const Vec2D &ta,const Vec2D &tb)
49 {
50 return Vec2D(ta.x+tb.x,ta.y+tb.y);
51 }
52 friend Vec2D operator-(const Vec2D &ta,const Vec2D &tb)
53 {
54 return Vec2D(ta.x-tb.x,ta.y-tb.y);
55 }
56 Vec2D operator=(const Vec2D &ta)
57 {
58 x=ta.x,y=ta.y;
59 return *this;
60 }
61 };
62 struct LineSeg ///线段,重载了/作为叉乘运算符,*作为点乘运算符
63 {
64 Point s,e;
65 LineSeg(){s=Point(0,0),e=Point(0,0);}
66 LineSeg(Point a, Point b){s=a,e=b;}
67 double lenth(void)
68 {
69 return sqrt((s.x-e.x)*(s.x-e.x)+(s.y-e.y)*(s.y-e.y));
70 }
71 friend double operator*(const LineSeg &ta,const LineSeg &tb)
72 {
73 return (ta.e.x-ta.s.x)*(tb.e.x-tb.s.x)+(ta.e.y-ta.s.y)*(tb.e.y-tb.s.y);
74 }
75 friend double operator/(const LineSeg &ta,const LineSeg &tb)
76 {
77 return (ta.e.x-ta.s.x)*(tb.e.y-tb.s.y)-(ta.e.y-ta.s.y)*(tb.e.x-tb.s.x);
78 }
79 LineSeg operator=(const LineSeg &ta)
80 {
81 s=ta.s,e=ta.e;
82 return *this;
83 }
84 };
85 struct Line /// 直线的解析方程 a*x+b*y+c=0 为统一表示,约定 a >= 0
86 {
87 double a,b,c;
88 Line(double d1=1, double d2=-1, double d3=0){ a=d1,b=d2,c=d3;}
89 };
90
91
92 int sgn(double ta,double tb);
93 double getdis(const Point &ta,const Point &tb);
94 double fArea(Point &ta,Point &tb,Point &tc);
95 bool intersect(LineSeg &lx,LineSeg &ly);
96 bool intersection(LineSeg &lx,LineSeg &ly,Point &pt);
97 bool cmp(const Point &ta,const Point &tb);
98 void graham(Point ps[],Point tb[],int n,int &num);
99 void ConvexClosure(Point ps[],Point tb[],int n,int &num);
100
101
102
103 int main(void)
104 {
105 int n;
106 double ans;
107 Point cs1,cs2;
108 LineSeg lx,ly,lz;
109 cin>>n;
110 while(n--)
111 {
112 ans=0;
113 cin>>lx.s.x>>lx.s.y>>lx.e.x>>lx.e.y;
114 cin>>ly.s.x>>ly.s.y>>ly.e.x>>ly.e.y;
115 if(lx.s.y>lx.e.y)
116 swap(lx.s,lx.e);
117 if(ly.s.y>ly.e.y)
118 swap(ly.s,ly.e);
119 lz=LineSeg(Point(-1,0),Point(0,0));
120 if(sgn(lx.s.y,lx.e.y)&&sgn(ly.s.y,ly.e.y)&&intersect(lx,ly)&&intersection(lx,ly,cs1))
121 {
122 if(sgn(lz*lx/lx.lenth(),lz*ly/ly.lenth())<0)
123 swap(lx,ly);
124 if( (sgn(lx.e.x,cs1.x)>=0 && sgn(ly.e.x,cs1.x)>=0 && sgn(ly.e.x,lx.e.x)<0)
125 || (sgn(lx.e.x,cs1.x)<=0 && sgn(ly.e.x,cs1.x)<=0 && sgn(lx.e.x,ly.e.x)>0)
126 || (sgn(lx.e.x,cs1.x)>=0 && sgn(ly.e.x,cs1.x)<=0))
127 {
128 if(lx.e.y>=ly.e.y)
129 {
130 lz=LineSeg(ly.e,Point(lx.e.x,ly.e.y));
131 intersection(lx,lz,cs2);
132 ans=fArea(cs1,cs2,ly.e);
133 }
134 else
135 {
136 lz=LineSeg(lx.e,Point(ly.e.x,lx.e.y));
137 intersection(ly,lz,cs2);
138 ans=fArea(cs1,cs2,lx.e);
139 }
140 }
141 }
142 printf("%.2f\n",ans+eps);
143
144 }
145
146 return 0;
147 }
148
149
150
151
152
153 /*******判断ta与tb的大小关系*******/
154 int sgn(double ta,double tb)
155 {
156 if(fabs(ta-tb)<eps)return 0;
157 if(ta<tb) return -1;
158 return 1;
159 }
160 /*********求两点的距离*************/
161 double getdis(const Point &ta,const Point &tb)
162 {
163 return sqrt((ta.x-tb.x)*(ta.x-tb.x)+(ta.y-tb.y)*(ta.y-tb.y));
164 }
165 /************三角形面积**************************/
166 double fArea(Point &ta,Point &tb,Point &tc)
167 {
168 return fabs(LineSeg(ta,tb)/LineSeg(ta,tc)*0.5);
169 }
170
171 /*********** 判断P1P2是否和P3P4相交****************************
172 其中Pi坐标为(xi,yi),需要满足两个条件:
173 (1)快速排斥试验:
174 以P1P2为对角线的矩形S1是否和以P3P4为对角线的矩形S2相交,
175 即 min(x1,x2)<=max(x3,x4) && min(x3,x4)<=max(x1,x2)
176 && min(y1,y2)<=max(y3,y4) &&min(y3,y4)<=max(y1,y2)
177 (2)跨立试验:
178 点P1,P2必然在线段P3P4的不同侧,
179 点P3,P4必然在线段P1P2的不同侧,
180 ***************************************************************/
181 bool intersect(LineSeg &lx,LineSeg &ly)
182 {
183 return sgn(min(lx.s.x,lx.e.x),max(ly.s.x,ly.e.x))<=0
184 && sgn(min(ly.s.x,ly.e.x),max(lx.s.x,lx.e.x))<=0
185 && sgn(min(lx.s.y,lx.e.y),max(ly.s.y,ly.e.y))<=0
186 && sgn(min(ly.s.y,ly.e.y),max(lx.s.y,lx.e.y))<=0
187 && sgn((lx/LineSeg(lx.s,ly.s))*(lx/LineSeg(lx.s,ly.e)),0)<=0
188 && sgn((ly/LineSeg(ly.s,lx.s))*(ly/LineSeg(ly.s,lx.e)),0)<=0;
189 }
190 /************线段求交点**************************
191 返回-1代表直线平行,返回0代表直线重合,返回1代表线段相交
192 利用叉积求得点P分线段DC的比,
193 然后利用高中学习的定比分点坐标公式求得分点P的坐标
194 **************************************************/
195 bool intersection(LineSeg &lx,LineSeg &ly,Point &pt)
196 {
197 pt=lx.s;
198 if(sgn(lx/ly,0)==0)
199 {
200 if(sgn(LineSeg(lx.s,ly.e)/ly,0)==0)
201 return 0;//重合
202 return -1;//平行
203 }
204 double t = (LineSeg(lx.s,ly.s)/ly)/(lx/ly);
205 pt.x+=(lx.e.x-lx.s.x)*t, pt.y+=(lx.e.y-lx.s.y)*t;
206 return 1;
207 }
208 /** ************凸包算法****************
209 寻找凸包的graham 扫描法
210 PS(PointSet)为输入的点集;
211 tb为输出的凸包上的点集,按照逆时针方向排列;
212 n为PointSet中的点的数目
213 num为输出的凸包上的点的个数
214 ****************************************** **/
215 bool cmp(const Point &ta,const Point &tb)/// 选取与最后一条确定边夹角最小的点,即余弦值最大者
216 {
217 // double tmp=LineSeg(ps[0],ta)/LineSeg(ps[0],tb);
218 // if(sgn(tmp,0)==0)
219 // return getdis(ps[0],ta)<getdis(ps[0],tb);
220 // else if(tmp>0)
221 // return 1;
222 return 0;
223 }
224 void graham(Point ps[],Point tb[],int n,int &num)
225 {
226 int cur=0,top=2;
227 for(int i=1;i<n;i++)
228 if(sgn(ps[cur].y,ps[i].y)>0 || (sgn(ps[cur].y,ps[i].y)==0 && sgn(ps[cur].x,ps[i].x)>0))
229 cur=i;
230 swap(ps[cur],ps[0]);
231 sort(ps+1,ps+n,cmp);
232 tb[0]=ps[0],tb[1]=ps[1],tb[2]=ps[2];
233 for(int i=3;i<n;i++)
234 {
235 while(sgn(LineSeg(tb[top-1],tb[top])/LineSeg(tb[top-1],ps[i]),0)<0)
236 top--;
237 tb[++top]=ps[i];
238 }
239 num=top+1;
240 }
241 /** 卷包裹法求点集凸壳,参数说明同graham算法 **/
242 void ConvexClosure(Point ps[],Point tb[],int n,int &num)
243 {
244 LineSeg lx,ly;
245 int cur,ch;
246 bool vis[Max];
247 num=-1,cur=0;
248 memset(vis,0,sizeof(vis));
249 for(int i=1;i<n;i++)
250 if(sgn(ps[cur].y,ps[i].y)>0 || (sgn(ps[cur].y,ps[i].y)==0 && sgn(ps[cur].x,ps[i].x)>0))
251 cur=i;
252 tb[++num]=ps[cur];
253 lx.s=Point(ps[cur].x-1,ps[cur].y),lx.e=ps[cur];
254 /// 选取与最后一条确定边夹角最小的点,即余弦值最大者
255 while(1)
256 {
257 double mxcross=-2,midis,tmxcross;
258 ly.s=lx.e;
259 for(int i=0;i<n;i++)if(!vis[i])
260 {
261 ly.e=ps[i];
262 tmxcross=(lx*ly)/lx.lenth()/ly.lenth();
263 if(sgn(tmxcross,mxcross)>0 ||(sgn(tmxcross,mxcross)==0 && getdis(ly.s,ly.e)<midis))
264 mxcross=tmxcross,midis=getdis(ly.s,ly.e),ch=i;
265 }
266 if(ch==cur)break;
267 tb[++num]=ps[ch],vis[ch]=1;
268 lx.s=tb[num-1],lx.e=tb[num],ly.s=tb[num];
269 }
270 }
标签:image 分享 eal 0ms mat section arm operator 表示
原文地址:http://www.cnblogs.com/weeping/p/6363707.html