题目描述
地平线(x轴)上有n个矩(lou)形(fang),用三个整数h[i],l[i],r[i]来表示第i个矩形:矩形左下角为(l[i],0),右上角为(r[i],h[i])。地平线高度为0。在轮廓线长度最小的前提下,从左到右输出轮廓线。
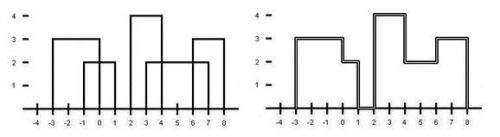
下图为样例2。
输入输出格式
输入格式:
第一行一个整数n,表示矩形个数
以下n行,每行3个整数h[i],l[i],r[i]表示第i个矩形。
输出格式:
第一行一个整数m,表示节点个数
以下m行,每行一个坐标表示轮廓线上的节点。从左到右遍历轮廓线并顺序输出节点。第一个和最后一个节点的y坐标必然为0。
输入输出样例
【样例输入1】 2 3 0 2 4 1 3 【样例输入2】 5 3 -3 0 2 -1 1 4 2 4 2 3 7 3 6 8
【样例输出1】 6 0 0 0 3 1 3 1 4 3 4 3 0 【样例输出2】 14 -3 0 -3 3 0 3 0 2 1 2 1 0 2 0 2 4 4 4 4 2 6 2 6 3 8 3 8 0
说明
【数据范围】
对于30%的数据,n<=100
对于另外30%的数据,n<=100000,1<=h[i],l[i],r[i]<=1000
对于100%的数据,1<=n<=100000,1<=h[i]<=10^9,-10^9<=l[i]<r[i]<=10^9
两种解法
这些都是看了学长的博客再写出来的,但是我觉得他写的不够碉,我看不懂,于是我也来写一个
第一种
扫描线+堆,我不会扫描线,现学的picture(poj1177),几近崩溃,后来回到这个题上发现这里用到的扫描线也不过如此。
堆,用的是stl里的multiset,他们说这个可以自己排序,还能当堆使,很神奇
仔细想想这个题,有很多种情况
这诸多情况,真是想想就头疼。
但是扫描线,再加上堆的强大援助就能解决
下面我就用十分通俗的语言讲解我的思路
扫描线,就是每一条竖着的线,楼房左侧的线叫入边,右侧的线叫出边,扫描线有长度(高度)up,横坐标x和出入边的标识k(k=1为入边,k=2为出边)。
struct line{ int up,x,k; }l[200020];
把所有竖边都加入扫描线后,就进行排序,排序要按照从左到右的顺序
如果横坐标相同,入边在先,出边在后
如果同为入边,高的在先,矮的在后,防遮挡
如果同为出边,矮的在先,高的在后,防遮挡
int cmp(line i,line j){ if(i.x!=j.x)return i.x<j.x; if(i.k!=j.k)return i.k<j.k; if(i.k==1)return i.up>j.up; if(i.k==2)return i.up<j.up; }
通过对图形的分析,我们发现,能够参与答案的只有目前的最高点,
所以我们对于入边只需要堆的最大值,其他的尽管加上
对于出边只需要判断一下是否是此刻的最大值,然后加加删删
完整代码

#include<iostream> #include<set> #include<algorithm> using namespace std; int n; struct build{ int h,l,r; }a[100010]; struct line{ int up,x,k; }l[200020]; int cnt,num; struct ANS{ int ax,ay; }ans[400040]; multiset<int>s; int cmp(line i,line j){ if(i.x!=j.x)return i.x<j.x; if(i.k!=j.k)return i.k<j.k; if(i.k==1)return i.up>j.up; if(i.k==2)return i.up<j.up; } int main(){ cin>>n; for(int i=1;i<=n;i++){ cin>>a[i].h>>a[i].l>>a[i].r; l[++cnt].up=a[i].h,l[cnt].x=a[i].l,l[cnt].k=1; l[++cnt].up=a[i].h,l[cnt].x=a[i].r,l[cnt].k=2; } sort(l+1,l+cnt+1,cmp); s.insert(0); for(int i=1;i<=cnt;i++){ int mx=*s.rbegin(); if(l[i].k==1){ if(l[i].up<=mx)s.insert(l[i].up); else{ ++num;ans[num].ax=l[i].x;ans[num].ay=mx; ++num;ans[num].ax=l[i].x;ans[num].ay=l[i].up; s.insert(l[i].up); } } if(l[i].k==2){ if(l[i].up==mx&&s.count(mx)==1){ s.erase(mx); ++num;ans[num].ax=l[i].x;ans[num].ay=l[i].up; ++num;ans[num].ax=l[i].x;ans[num].ay=*s.rbegin(); } else s.erase(s.find(l[i].up)); } } cout<<num<<endl; for(int i=1;i<=num;i++){ cout<<ans[i].ax<<‘ ‘<<ans[i].ay<<endl; } }
第二种
线段树,不感兴趣

/* 离散化+线段树+模拟 由于数据量太大,我们先把所有的墙壁离散化,用线段树维护每个离散化后的横坐标的最高点, 然后模拟求出答案。 */ #include<cstdio> #include<iostream> #include<algorithm> #define lson l,m,now*2 #define rson m+1,r,now*2+1 #define M 200010 using namespace std; int mx[M*4],tag[M*4],a[M*2],b[M*2],ans1[M*5],ans2[M*5],n,cnt=1; struct node { int x,y,h; };node q[M]; int read() { char c=getchar();int num=0,flag=1; while(c<‘0‘||c>‘9‘){if(c==‘-‘)flag=-1;c=getchar();} while(c>=‘0‘&&c<=‘9‘){num=num*10+c-‘0‘;c=getchar();} return num*flag; } void push_up(int now) { mx[now]=max(mx[now*2],mx[now*2+1]); } void push_down(int now) { if(!tag[now])return; tag[now*2]=max(tag[now],tag[now*2]); tag[now*2+1]=max(tag[now],tag[now*2+1]); mx[now*2]=max(tag[now],mx[now*2]); mx[now*2+1]=max(tag[now],mx[now*2+1]); tag[now]=0; } void change(int x,int y,int v,int l,int r,int now) { if(l>=x&&r<=y) { mx[now]=max(mx[now],v); tag[now]=max(tag[now],v); return; } push_down(now); int m=(l+r)/2; if(m>=x)change(x,y,v,lson); if(y>m)change(x,y,v,rson); push_up(now); } int query(int x,int l,int r,int now) { if(l==r)return mx[now]; int m=(l+r)/2; push_down(now); if(x<=m)return query(x,lson); else return query(x,rson); } int main() { n=read(); for(int i=1;i<=n;i++) { scanf("%d%d%d",&q[i].h,&q[i].x,&q[i].y); a[i*2-1]=q[i].x;a[2*i]=q[i].y; } sort(a+1,a+2*n+1);b[1]=a[1]; for(int i=2;i<=2*n;i++) if(a[i]!=a[i-1])b[++cnt]=a[i]; for(int i=1;i<=n;i++) { int x=lower_bound(b+1,b+cnt+1,q[i].x)-b; int y=lower_bound(b+1,b+cnt+1,q[i].y)-b; change(x,y-1,q[i].h,1,cnt,1); } int tot=0; for(int i=1;i<=cnt;i++) { ans1[i]=b[i];ans2[i]=query(i,1,cnt,1); if(ans2[i]!=ans2[i-1])tot++; } printf("%d\n",tot*2); for(int i=1;i<=cnt;i++) if(ans2[i]!=ans2[i-1]) { printf("%d %d\n",ans1[i],ans2[i-1]); printf("%d %d\n",ans1[i],ans2[i]); } return 0; }

