标签：示例 矩阵 density 决定 连通性 演示 密度 放弃 部分
作为OCR系统的第一步，特征提取是希望找出图像中候选的文字区域特征，以便我们在第二步 进行文字定位和第三步进行识别。在这部分内容中，我们集中精力模仿肉眼对图像与汉字的处理过程，在图像的处理和汉字的定位方面走了一条创新的道路。这部分工作是整个OCR系统最核心的部分，也是我们工作中最核心的部分。
传统的文本分割思路大多数是“边缘检测 + 腐蚀膨胀 + 联通区域检测”，如论文[1]。 然而，在复杂背景的图像下进行边缘检测会导致背景部分的边缘过多(即噪音增加)，同时文字部分的边缘 信息则容易被忽略，从而导致效果变差。 如果在此时进行腐蚀或膨胀，那么将会使得背景区域跟文字区域粘合，效果进一步恶化。（事实上，我们在这条路上已经走得足够远了，我们甚至自己写过边缘检测函数来做这个事情，经过很多测试，最终我们决定放弃这种思路。）
因此，在本文中，我们放弃了边缘检测和腐蚀膨胀，通过聚类、分割、去噪、池化等步骤，得到了比较良好的文字部分的特征，整个流程大致如图2，这些特征甚至可以直接输入到文字识 别模型中进行识别，而不用做额外的处理。由于我们每一部分结果都有相应的理论基础作为支撑，因此能够模型的可靠性得到保证。
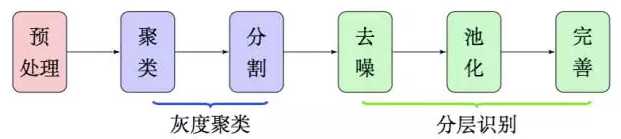
图2：特征提取大概流程
在这部分的实验中，我们以图3来演示我们的效果。这个图像的特点是尺寸中等，背景较炫，色彩较为丰富，并且文字跟图片混合排版，排版格式不固定，是比较典型的电商类宣传图片。可以看到，处理这张图片的要点就是如何识别图片区域和文字区域，识别并剔除右端的电饭锅，只保留文字区域。
图3：小米电饭锅介绍图
图像的预处理
首先，我们将原始图片以灰度图像的形式读入，得到一个的灰度矩阵，其中m, n 是图像的长、宽。这样读入比直接读入RGB彩色图像维度更低，同时没有明显损失文字信息。转换为灰度图事实上就是将原来的RGB图像的三个通道以下面的公式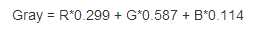
整合为一个通道：
图3的灰度图如下图
图像本身的尺寸不大，如果直接处理，则会导致文字笔画过小，容易被当成噪音处理掉，因此为了保证文字的笔画有一定的厚度，可以先将图片进行放大。 在我们的实验中，一般将图像放大为原来的两倍就有比较好的效果了。
不过，图像放大之后，文字与背景之间的区分度降低了。这是因为图片放大时会使用插值算法来填补空缺部分的像素。这时候需要相应地增大区分度。经过测试，在大多数图片中，使用次数为2的“幂次变换”效果较好。幂次变换为
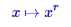（2）
其中x代表矩阵M中的元素，r为次数，在这里我们选取为2。 然后需要将结果映射到[0,255]区间：
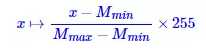（3）
其中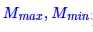 
是矩阵的最大值和最小值。
灰色聚类
接着我们就对图像的色彩进行聚类。聚类的有两个事实依据：
灰度分辨率 肉眼的灰度分辨率大概为40，因此对于像素值254和255，在我们肉眼看来都 只是白色；
设计原则 根据我们一般的审美原则，在考虑海报设计、服装搭配等搭配的时候，一般要 求在服装、海报等颜色搭配不超过三种颜色。
更通俗地说，虽然灰度图片色阶范围是[0, 255]，但我们能感觉到的整体的色调一般不多，因此，可以将相近的色阶归为一类，从而减少颜色分布，有效地降低噪音。
事实上，聚类是根据图像的特点自适应地进行多值化的过程，避免了传统的简单二值化所带来 的信息损失。由于我们需要自动地确定聚类数目，因此传统的KMeans等聚类方法被我们抛弃 了，而且经过我们测试，诸如MeanShift等可行的聚类方法又存在速度较慢等缺陷。因此，我们 自行设计了聚类方法，使用的是“核概率密度估计”的思路，通过求颜色密度极值的方式来聚类。
核密度估计 经过预处理的图像，我们可以对每个色阶的出现次数进行统计，得到如图5的频率分布直方图：
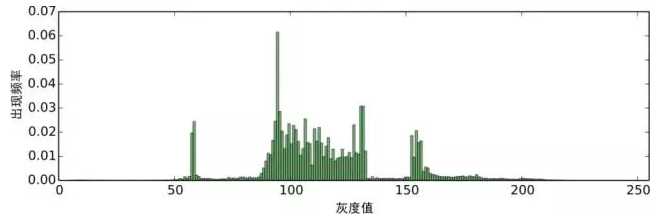
图5：对预处理后的图像进行灰色阶统计
可以看到，色阶的分布形成了几个比较突出的峰，换言之，存在一定的聚类趋势。 然而，直方 图的统计结果是不连续的，一个平滑的结果更便于我们分析研究，结果也更有说服力。 将统计 结果平滑化的方法，就是核密度估计(kernel density estimation)。
核密度估计方法是一种非参数估计方法，由Rosenblatt和Parzen提出，在统计学理论和应用领 域均受到高度的重视[2]。 当然，也可以简单地将它看成一种函数平滑方式。 我们根据大量的数据 来估计某个值出现的概率(密度)时，事实上做的是如下估算：
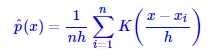（4）
其中K(x)称为核函数。 当 取为1，且K(x)取
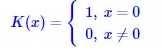（5）
时，就是我们上述的直方图估计。 K(x)这一项的含义很简单，它就是告诉我们在范围h内的都算入到x中去，至于怎么算，由
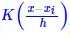给出。可见，h的选择对结果的影响很大，h我们称之为带宽(bandwidth)，它主要影响结果的平滑性。 如果K(x)是离散的，得到的结果还是离散的，但如果K(x)是光滑的，得到的结果也是比较光滑的。一个常用的光滑函数核是高斯核：
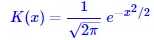（6）
所得到的估计也叫高斯核密度估计。 在这里，我们使用scott规则自适应地选取 ，但需要手动指定一个平滑因子，在本文中，我们选取为0。2。对于示例图片，我们得到如图6的红色曲线的结果。
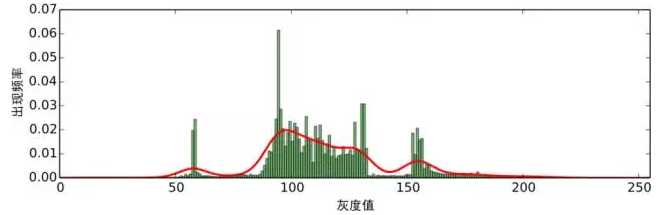
图6：频率分布的高斯核密度估计
极大极小值分割
从图6中我们进一步可以看出，图像确实存在着聚类趋势。 这表现为它有几个明显的极大值和极 小值点，这里的极大值点位于x = 10, 57, 97, 123, 154，极小值点位于25, 71, 121, 142。
因此，一个很自然的聚类方法是：有多少个极大值点，就聚为多少类，并且以极小值点作为类 别之间的边界。 也就是说，对于图3，可以将图像分层5层，逐层处理。 分层之后，每一层的形状 如下图，其中白色是1，黑色是0。
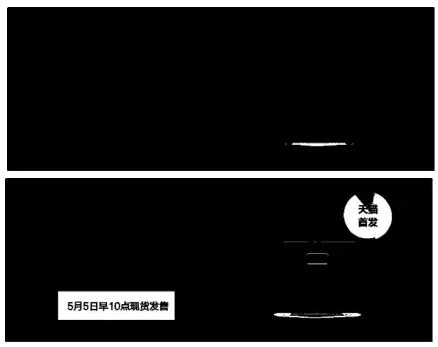
通过聚类将图像分为5个图层
可见，由于“对比度”和“渐变性”假设，通过聚类确实可以将文字图层通过核密度估计的聚类方 法分离开来。 而且，通过聚类分层的思路，无需对文字颜色作任何假定，即便是文字颜色跟背 景颜色一致时，也可以获得有效检测。
逐层识别
当图像有效地进行分层后，我们就可以根据前面的假设，进一步设计相应的模型，通过逐层处 理的方式找出图像中的文字区域。
连通性
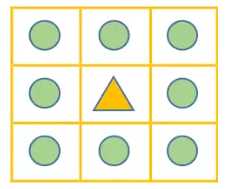
可以看到，每一层的图像是由若干连通区域组成的，文字本身是由笔画较 为密集组成的，因此往往文字也能够组成一个连通区域。这里的连通定义为 8邻接，即某个像素周围的8个像素都定义为邻接像素，邻接的像素则被定 义为同一个连通区域。
定义了连通区域后，每个图层被分割为若干个连通区域，也就是说，我们 逐步地将原始图像进行分解，如图9。
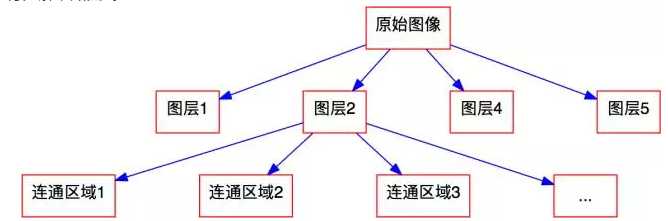
图9 图像分解结构图
抗腐蚀能力 将图像分解至连通区域这一粒度后，我们就不再细分了，下一步开始识别哪些区域是可能的文字区域。 这里我们要求文字具有一定的抗腐蚀能力。 因此我们先来定义腐蚀。
腐蚀是一种图像上的形态学变换，一般针对于二值图像，对于二值图像中的非零像素(即取值为 1的像素)，如果它邻接的像素都为1，则保持不变，否则变为0，这里我们同样采用的是8邻接的 定义。 可以看到，如果连通区域的边界线越长，那么腐蚀运算对它的“伤害”就越大，反之，如果 连通区域的边界线越短，那么腐蚀运算对它的“伤害”就越小。
根据以上腐蚀的定义，我们可以给出一个对文字区域的要求：
抗腐蚀要求 文字所在的连通区域应当具有一定的抗腐蚀能力。
这里的“一定”是指在一个连续的范围内，不能太大，也不能太小。 比如，一个面积较大的方形区 域，它的抗腐蚀能力是很强的，因为它边界线很短，但这些区域明显不是文字区域，上一篇文 章中分解后图层5的电饭锅便是属于这一类型；此外，抗腐蚀能力太弱也不可以，比如细长的 线条，腐蚀之后可能就消失了，这些也不作为候选的文字区域，上一篇文章中分解后图层4的 文字边界线就属于这一类型。
这里可以定义一个抗腐蚀能力的指标：
连通区域的抗腐蚀能力 = 该区域被腐蚀后的总面积/该区域被腐蚀前的总面积 (7)
经过测试，文字区域的抗腐蚀能力大概在[0.1, 0.9]这个区间中。
经过抗腐蚀能力筛选分解的5个图层，得到如下图的特征层。
只保留抗腐蚀能力在[0。1, 0。9]这个区间中的连通区域
池化操作 到现在为止，我们得到了5个特征层，虽然肉眼可以看到，文字主要集中在第5个特征层。但是，对于一般的图片，文字可能分布在多个特征层，因此需要对特征层进行整合。我们这里进行特征整合的方法，类似于卷积神经网络中的“池化”，因此我们也借用了这个名称。 首先，我们将5个特征层进行叠加，得到一幅整体的图像特征(称为叠加特征)。这样的图像特征可以当作最后的特征输出，但并不是最好的方法。我们认为，某个区域内的主要文字特征应该已经集中分布在某个特征层中，而不是分散在所有的特征层。因此，得到叠加特征后，使用类 似“最大值池化”的方式整合特征，步骤如下：
1。直接叠加特征，然后对叠加特征划分连通区域；
2。检测每个连通区域的主要贡献是哪个特征层，该连通区域就只保留这个特征层的来源。
经过这样的池化操作后，得到的最终特征结果如图11。
图11 池化后的特征
后期处理
对于我们演示的这幅图像，经过上述操作后，得到的特征图11已经不用再做什么处理了。 然而， 对于一般的图片，还有可能出现一些没处理好的区域，这时候需要在前述结果的基础上进一步 排除。 排除过程主要有两个步骤，一个是低/高密度区排除，另外则是孤立区排除。
密度排除 一种明显不是文字区域的连通区域是低密度区，一个典型的例子就是由表格线组成的连通区域，这样的区域范围较大，但点很少，也就是密度很低，这种低密度区可以排除。 首先我们来定义连通区域密度和低密度区：
连通区域密度 从一个连通区域出发，可以找到该连通区域的水平外切矩形，该区域的密度定义为
连通区域密度 =连通区域的面积/外切矩形的面积×原图像总面积/外切矩形的面积 (8)
低密度区 如果一个连通区域的密度小于16，那么这个连通区域定义为低密度区。
直觉上的定义应该是连通区域的面积 / 外切矩形的面积，但这里多了一个因子原图像总面积 / 外切矩形的面积，目的是把面积大小这个影响因素加进去，因为文字一般有明显的边界，容易被分割开来，所以一般来说面积越大的区域越不可能是文本区域。这里的参数16是经验值。 低密度区排除是排除表格等线条较多的非文字区域的有效方法。类似地，范围较大的高密度区也是一类需要排除的区域。 有了低密度区之后，就很容易定义高密度区了：
高密度区定义* 如果一个连通区域以水平外切矩形反转后的区域是一个低密度区，那个这个 连通区域定义为高密度区。
这个定义是很自然的，但是却有一定的不合理性。比如“一”字，是一个水平的矩形，于是翻转后 的密度为0，于是这个“一”字就被排除了，这是不合理的。 解决这个问题的一个方案是：
高密度区定义 当且仅当下面条件满足时才被定义为高密度区：
（矩形的面积 ?连通区域的面积）/外切矩形的面积× 外切矩形的面积/原图像总面积< 16 （9）
这是在原来定义的基础上加上了1，防止了翻转后密度为0的情况。
还有另外一种失效的情况，就是假如输入图片是单字图片，那么只有一个连通区域，且原图像总面积 外切矩形的面积接近于1，因此它就被判为低密度区，这样就排除了单字。这种情形确实比较难兼顾。一个可行的解决办法是通过人工指定是单字模式、单行模型还是整体图片模式，Google的Tesseract OCR也提供了这样的选项。
孤立区
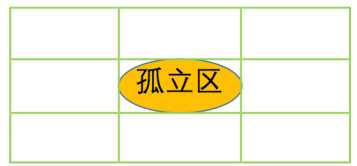
孤立区排除的出发点是：文字之间、笔画之间应该是比较紧 凑的，如果一个区域明显地孤立于其他区域，那么这个区域 很可能不是文字区域。 也就是说，可以把孤立区给排除掉。 首 先我们定义孤立区的概念：
孤立区 从一个连通区域出发，可以找到该连通区域的水平外切矩形，将这个矩形中心对称 地向外扩张为原来的9倍(长、宽变为原来的3倍，如左图)，扩展后的区域如果没有包含其他 的连通区域，那么原来的连通区域称为孤立区。
在大多数情况，孤立区排除是一种非常简单有效的去噪方法，因为很多噪音点都是孤立区。 但是孤立区排除是会存在一定风险的。 如果一幅图像只有一个文字，构成了唯一一个连通区域， 那么这个连通区域就是孤立的，于是这个文字就被排除了。因此，要对孤立区加上更多的限制，一个可选的额外限制是：被排除的孤立区的占连通区域的面积 / 外切矩形的面积要大于0.75（这个值源于圆与外切正方形的面积之比 π / 4）。
标签：示例 矩阵 density 决定 连通性 演示 密度 放弃 部分
原文地址：http://www.cnblogs.com/sumuncle/p/6369281.html
