标签:style http 使用 io strong ar div cti
二补数(2‘s complement)是一种用二进制表示有号数的方法,也是一种将数字的正负号变号的方式,常在计算机科学中使用。在中国大陆称作补码,台湾和香港称为二补数。
一个数字的二补数就是将该数字作比特反相运算(即一补数或反码),再将结果加 1。在二补数系统中,一个负数就是用其对应正数的二补数来表示。
二补数系统的最大优点是可以在加法或减法处理中,不需因为数字的正负而使用不同的计算方式。只要一种加法电路就可以处理各种有号数加法,而且减法可以用一个数加上另一个数的二补数来表示,因此只要有加法电路及二补数电路即可完成各种有号数加法及减法,在电路设计上相当方便。
另外,二补数系统的 0 只有一个表示方式,这点和一补数系统不同(在一补数系统中,0 有二种表示方式),因此在判断数字是否为 0 时,只要比较一次即可。
右侧的表是一些 8-bit 二补数系统的整数。它的可表示的范围包括-128到127,总共256 (28)个整数。
以下用 4 比特的二补数数字来说明二补数系统的数字表示方式。
以上的表示方式在电脑处理时格外方便,用以下的例子说明:
0011 (3) + 1111 (-1) -------------- 10010 (2)
结果 10010 似乎是错的,因为已经超过四个比特,不过若忽略掉(从右数起的)第 5 个比特,结果是 0010 (2),和我们计算的结果一样。而且若可以将二进制的 0001 (1) 变号为 1111 (-1),以上的式子也可以计算减法:3-1 = 2。
在 n 比特的二补数加减法中,忽略第 n+1 个比特的作法在各种有号数加法下都适用(不过在判断是否溢出(overflow) 时,仍然会用到第 n+1 个比特)。因此在二补数的系统,加法电路就可以处理有负数的加法,不需另外处理减法的电路。而且,只要有电路负责数字的变号(例如将 1 变换为 -1),也可以用加法电路来处理减法。而数字的变号就用计算数字的二补数来完成。
在一般 n 比特的二进制数字中,最高有效比特(MSB) 第 n 比特代表的数字为 2n−1。不过,在 n 比特的二补数系统中,最高有效比特(MSB) 第 n 比特表示符号比特,若符号比特为 0,数字为正数或 0,若符号比特为 1,数字为负数。以下是 n 比特的二补数系统中,几个特别的数字:
| 二补数 | 实际数字 | 附注 |
|---|---|---|
| 0 111....111 | 2n−1-1 | 最大正数 |
| ... | ... | |
| 0 000....001 | 1 | |
| 0 000....000 | 0 | |
| 1 111....111 | -1 | |
| ... | ... | |
| 1 000....001 | -2n−1+1 | |
| 1 000....000 | -2n−1 | 最小负数 |
因此,在 8 比特的二补数系统中,可以表示的最大正数为 28−1-1 = 127,可以表示最小的负数为 -28−1 = -128
在计算二进制数字的二补数时,会将数字进行比特反相运算,再将结果加 1,不考虑溢出比特(一般情形,溢出比特会为 0),就可以得到该数字的二补数。
以下考虑用有号数 8 比特二进制表示的数字 5:
其最高比特为 0,因为此数字为正数。若要用二补数系统表示 -5,首先要将 5 的二进制进行反相运算〔1 变为 0,0 变为 1 〕:
目前的数字是数字 5 的一补数,因此需要再加 1,才是二补数:
以上就是在二补数系统中 -5 的表示方式。其其最高比特为 1,因为此数字确实为负数。
一个负数的二补数就是其对应的正数。以 -5 为例,先求数字的一补数:
再加一就是 -5 的二补数,也就是 5。
简单来说,数字 a (正负数皆可)的二补数即为 -a。
若要计算 n 位数二补数二进制对应的十进制,需要知道每位数对应的数字,除了最高比特外,其他比特的对应数字均和一般二进制相同,即第 i 位数表示数字 2i−1。但最高比特若为 1 时,其表示数字为 -2n−1,因此若用此方式计算 0000 0101 表示的数字,其结果为:
有二个数字的二补数等于本身:一个是 0,另一个为该比特可表示最大绝对值负数(即 1000...000)。
0 的二补数计算方式(以 8 比特为例) 如下:先计算它的一补数:
再将一补数加一:
忽略溢出,其结果为 0(0 是唯一计算二补数过程中会出现溢出的数字。)。因此 0 的二补数为 0。而 0 x (-1) = 0,因此其二补数仍满足“数字 a 的二补数为 -a”的原则。
若计算 1000 0000 (-128、8 比特可表示最大绝对值负数)的二补数:先计算它的一补数:
再加一就是它的二补数。
1000 0000 (-128)的二补数仍为 1000 0000 (-128)。但 (-128) x (-1) = 128,因此其二补数是以上规则的例外。
其例外原因为因为 8 比特的二补数数字范围为 -128 ~ 127。128 无法以 8 比特的二补数数字表示。在计算其他位数的最大绝对值负数(即 1000...000)时,也会有类似情形。
另一种正式计算一数字(以 -N 为例)的二补数 N* 的公式如下:
其中 N* 是 -N 的补数,而 n 是数字 -N 用二进制表示时需要的位数。
以八比特的“-123”为例:
-123 的二补数计算方式如下:



以另一种较简单的方式,可以找出二进制数字的二补数:
以 0011 1100 为例(图中的 ^ 表示目前转换的数字,-表示还不确定的位数):
原數字 二补数
0011 1100 ---- ---0 (此位元為 0)
^
0011 1100 ---- --00 (此位元為 0)
^
0011 1100 ---- -100 (找到第 1 個為 1 的位元)
^
0011 1100 1100 0100 (其餘位元直接反相)
^
因此其结果为 1100 0100
| 十进制 | 4 比特二补数 | 8 比特二补数 |
|---|---|---|
| 5 | 0101 | 0000 0101 |
| -3 | 1101 | 1111 1101 |
将一个特定比特二补数系统的数字要以较多比特表示时(例如,将一个字节的变量复制到另一个二个字节),所有增加的高比特都要填入原数字的符号比特。在一些微处理机中,有指令可以运行上述的动作。若是没有,需要自行在程序中处理。==>
在二补数系统中,当数字要向右位移几个比特时,在位移后需将符号比特再填入原位置(算术移位),保持符号比特不变。以下是二个例子:
數字 0010 1010 1010 1010 向右位移一次 0001 0101 1101 0101 向右位移二次 0000 1010 1110 1010
而当一个数字要向左位移n个比特时,最低比特填n个 0,权值最高的n个位被抛弃。以下是二个例子:
數字 0010 1010 1010 1010 向左位移一次 0101 0100 0101 0100 向左位移二次 1010 1000 1010 1000
向右位移一次相当于除以 2,利用算术移位的方式可以确保位移后的数字正负号和原数字相同,因为一数字除以 2 后,不会改变其正负号。 注意:向左位移一次相当于乘以2,虽然乘以在理论上并不会改变一个数的符号,但是在二补数系统中,用以表示数的二进制码长度有限,能够表示的数的范围也是有限的:若一个数的高权值上的数位已经被占用,此时再将这个数左移若干位(乘以2n)的话,有可能造成数位溢出(overflow),高权值上的数将会失去,对于绝对值很大数,这将造成整体表达的错误。
为什么二补数能这么巧妙实现了正负数的加减运算?答案是:指定n比特字长,那么就只有2n个可能的值,加减法运算都存在上溢出与下溢出的情况,实际上都等价于模2n的加减法运算。这对于n比特无符号整数类型或是n比特有符号整数类型都同样适用。
例如,8位无符号整数的值的范围是0到255. 因此4+254将上溢出,结果是2,即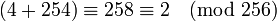 。
。
例如,8位有符号整数的值的范围,如果规定为−128到127, 则126+125将上溢出,结果是−5,即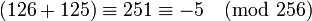 。
。
对于8位字长的有符号整数类型,以28即256为模,则
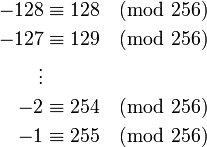
所以模256下的加减法,用0, 1, 2, …, 254,255表示其值,或者用−128, −127,… , −1, 0, 1, 2,… ,127是完全等价的。−128与128,−127与129,…,−2与254,−1与255可以互换而加减法的结果不变。从而,把8位(octet)的 高半部分(即二进制的1000 0000到1111 1111)解释为−128到−1,同样也实现了模256的加减法,而且所需要的CPU加法运算器的电路实现与8位无符号整数并无不同。
实际上对于8比特的存储单元,把它的取值[00000000, …, 11111111]解释为[0, 255], 或者[-1, 254], 或者[-2, 253], 或者[-128, 127], 或者[-200, 55], 甚至或者[500, 755], 对于加法硬件实现并无不同。
二补数系统数字的加法和一般加法相同,而且在运算完成后就可以看出结果的正负号,不需特别的处理。
正数与负数相加不会出现上溢错误,上溢错误只会在两个正数或两个负数相加时发生。
以 15 加 -5 为例:
11111 111 (进位) 0000 1111 (15) + 1111 1011 (-5) ================== 0000 1010 (10)
由于加数和被加数都是 8 比特,因此运算结果也限制在 8 比特内。第 8 比特相加后产生的进位不考虑(因为不存在第 9 比特)的 1 被忽略,所以其结果为 10。而 15 + (-5) = 10,计算结果正确。
在以上计算式中,可以由进位列的最左侧二个比特得知结果是否出现溢出。溢出就是数字的绝对值太大,以致于无法在指定的二进制比特个数来表示(在此例中,是超过 8 比特的范围)。若进位列的最左侧二个比特同为 0 或同为 1,表示结果正确,若是一个为 0,另一个为 1,表示出现溢出错误。也可以对此二个比特进行异或运算,结果为 1 时,表示出现溢出错误。以下以 7 + 3 的 4 比特加法说明溢出错误的情形。
0111 (进位) 0111 (7) + 0011 (3) ============= 1010 (−6) 結果不正確!
在此例中,进位列的最左侧二个比特为 01,因此出现溢出错误。溢出的原因是 7 + 3 的结果 (10) 超过二补数系统 4 比特所可以表示的数字范围 -8~7。
标签:style http 使用 io strong ar div cti
原文地址:http://www.cnblogs.com/milantgh/p/3925425.html