标签:matrix img ddd ifstream std visit 模拟 fst stack

不是有很多可以说的,记住不能变算边取min
1 #include<iostream> 2 #include<fstream> 3 #include<sstream> 4 #include<cstdio> 5 #include<cctype> 6 #include<cstring> 7 #include<cstdlib> 8 #include<cmath> 9 #include<algorithm> 10 #include<queue> 11 #include<vector> 12 #include<stack> 13 #include<map> 14 #include<set> 15 using namespace std; 16 typedef bool boolean; 17 #define INF 0xfffffff 18 #define smin(a, b) a = min(a, b) 19 #define smax(a, b) a = max(a, b) 20 21 ifstream fin("word.in"); 22 ofstream fout("word.out"); 23 24 int n; 25 int c; 26 char str[105]; 27 28 inline void init() { 29 fin >> str; 30 n = strlen(str); 31 } 32 33 int counter[30]; 34 inline void solve() { 35 int minv = 1000, maxv = 0; 36 memset(counter, 0, sizeof(counter)); 37 for(int i = 0, ch; i < n; i++) { 38 ch = (int) (str[i] - ‘a‘); 39 counter[ch]++; 40 } 41 for(int i = 0; i < 30; i++) { 42 if(counter[i] != 0) { 43 smin(minv, counter[i]); 44 smax(maxv, counter[i]); 45 } 46 } 47 c = maxv - minv; 48 if(c < 2) { 49 fout << "No Answer" << endl; 50 fout << 0 << endl; 51 } else if(c == 2 || c == 3) { 52 fout << "Lucky Word" << endl; 53 fout << c << endl; 54 } else { 55 int limit = (int)sqrt(c + 0.5); 56 for(int i = 2; i <= limit; i++) { 57 if(c % i == 0) { 58 fout << "No Answer" << endl; 59 fout << 0 << endl; 60 return; 61 } 62 } 63 fout << "Lucky Word" << endl; 64 fout << c << endl; 65 } 66 } 67 68 int main() { 69 init(); 70 solve(); 71 fin.close(); 72 fout.close(); 73 return 0; 74 }

记下每个数字所需的火柴数,然后去搜索吧,或者找出上界,枚举两个加数,再判断是否可行。
1 #include<iostream> 2 #include<fstream> 3 #include<sstream> 4 #include<cstdio> 5 #include<cctype> 6 #include<cstring> 7 #include<cstdlib> 8 #include<cmath> 9 #include<algorithm> 10 #include<queue> 11 #include<vector> 12 #include<stack> 13 #include<map> 14 #include<set> 15 using namespace std; 16 typedef bool boolean; 17 #define INF 0xfffffff 18 #define smin(a, b) a = min(a, b) 19 #define smax(a, b) a = max(a, b) 20 21 ifstream fin("matches.in"); 22 ofstream fout("matches.out"); 23 24 int n; 25 26 inline void init() { 27 fin >> n; 28 n -= 4; 29 } 30 31 const int cost[10] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6}; 32 33 int result = 0; 34 int buf[25]; 35 36 int getInt(int from, int end) { 37 if(buf[from] == 0 && end - from > 1) return -10000; 38 if(buf[from] == 0) return 0; 39 int ret = 0; 40 for(int i = from; i < end; i++) { 41 ret *= 10; 42 ret += buf[i]; 43 } 44 return ret; 45 } 46 47 int check(int top) { 48 int res = 0; 49 if(top < 3) return 0; 50 // if(buf[0] == 0 && buf[1] == 0) return (buf[2] == 0 && top == 3) ? (1) : (0); 51 for(int i = 1; i < top - 1; i++) { 52 for(int j = i + 1; j < top; j++) { 53 int a = getInt(0, i); 54 int b = getInt(i, j); 55 int c = getInt(j, top); 56 if(a + b == c) res++;//, fout << a << "+" << b << "=" << c << endl;; 57 } 58 } 59 return res; 60 } 61 62 void dfs(int pos, int used) { 63 if(used == n) { 64 result += check(pos); 65 return; 66 } 67 for(int i = 0; i <= 9; i++) { 68 if(used + cost[i] <= n) { 69 buf[pos] = i; 70 dfs(pos + 1, used + cost[i]); 71 } 72 } 73 } 74 75 inline void solve() { 76 dfs(0, 0); 77 fout << result; 78 fin.close(); 79 fout.close(); 80 } 81 82 int main() { 83 init(); 84 solve(); 85 return 0; 86 }

从下面传上来,等于从上面传下去,原问题就等于从左上角找两条互不相交的路径,简单地是写个dp,f[x0][y0][x1][y1]或者f[dis][x0][x1],然而我先想到的是网络流,将每个点拆成2个点(除去左上角的和右下角那个),中间连一条容量为1,费用为0的有向边。其他边按照题目意思来建。也是容量为1,费用为起点的点权。然后求左上角到右下角流量为2的最大费用流。(noip用网络流?)
1 #include<iostream> 2 #include<fstream> 3 #include<sstream> 4 #include<cstdio> 5 #include<cctype> 6 #include<cstring> 7 #include<cstdlib> 8 #include<cmath> 9 #include<algorithm> 10 #include<queue> 11 #include<vector> 12 #include<stack> 13 #include<map> 14 #include<set> 15 using namespace std; 16 typedef bool boolean; 17 #define inf 0xfffffff 18 #define smin(a, b) a = min(a, b) 19 #define smax(a, b) a = max(a, b) 20 21 typedef class Edge { 22 public: 23 int end; 24 int next; 25 int flow; 26 int cap; 27 int cost; 28 Edge(const int end = 0, const int next = 0, const int flow = 0, const int cap = 0, const int cost = 0):end(end), next(next), flow(flow), cap(cap), cost(cost) { } 29 }Edge; 30 31 typedef class MapManager { 32 public: 33 int ce; 34 int* h; 35 Edge* edge; 36 MapManager():ce(0), h(NULL), edge(NULL) { } 37 MapManager(int points, int limit):ce(0) { 38 h = new int[(const int)(points + 1)]; 39 edge = new Edge[(const int)(limit + 1)]; 40 memset(h, 0, sizeof(int) * (points + 1)); 41 } 42 inline void addEdge(int from, int end, int flow, int cap, int cost) { 43 edge[++ce] = Edge(end, h[from], flow, cap, cost); 44 h[from] = ce; 45 } 46 inline void addDoubleEdge(int from, int end, int cap, int cost) { 47 addEdge(from, end, 0, cap, cost); 48 addEdge(end, from, cap, cap, -cost); 49 } 50 Edge& operator [](int pos) { 51 return edge[pos]; 52 } 53 int reverse(int pos) { 54 return (pos & 1) ? (pos + 1) : (pos - 1); 55 } 56 }MapManager; 57 #define m_begin(g, i) (g).h[(i)] 58 59 ifstream fin("message.in"); 60 ofstream fout("message.out"); 61 62 int n, m; 63 MapManager g; 64 int l; 65 66 inline int pti(int x, int y) { return x * n + y; } 67 inline void init() { 68 fin >> m >> n; 69 g = MapManager(2 * m * n, 8 * m * n); 70 l = m * n; 71 for(int i = 0, a; i < m; i++) { 72 for(int j = 0; j < n; j++) { 73 fin >> a; 74 g.addDoubleEdge(pti(i, j), pti(i, j) + l, 1, 0); 75 if(i < m - 1) g.addDoubleEdge(pti(i, j) + l, pti(i + 1, j), 1, a); 76 if(j < n - 1) g.addDoubleEdge(pti(i, j) + l, pti(i, j + 1), 1, a); 77 } 78 } 79 } 80 81 int* dis; 82 boolean *visited; 83 int* last; 84 int* lase; 85 int* mflow; 86 int cost; 87 queue<int> que; 88 boolean spfa(int s, int t) { 89 memset(dis, 0xf0, sizeof(int) * (2 * l + 1)); 90 memset(visited, false, sizeof(boolean) * (2 * l + 1)); 91 dis[s] = last[s] = lase[s] = 0; 92 que.push(s); 93 mflow[s] = inf; 94 visited[s] = true; 95 while(!que.empty()) { 96 int e = que.front(); 97 que.pop(); 98 visited[e] = false; 99 for(int i = m_begin(g, e); i != 0; i = g[i].next) { 100 int& eu = g[i].end; 101 if(dis[e] + g[i].cost > dis[eu] && g[i].flow < g[i].cap) { 102 dis[eu] = dis[e] + g[i].cost; 103 last[eu] = e; 104 lase[eu] = i; 105 mflow[eu] = min(g[i].cap - g[i].flow, mflow[e]); 106 if(!visited[eu] && eu != t) { 107 que.push(eu); 108 visited[eu] = true; 109 } 110 } 111 } 112 } 113 if(!dis[t]) return false; 114 for(int i = t; i != s; i = last[i]) { 115 g[lase[i]].flow += mflow[t]; 116 g[g.reverse(lase[i])].flow -= mflow[t]; 117 cost += mflow[t] * g[lase[i]].cost; 118 } 119 return true; 120 } 121 122 inline void solve() { 123 dis = new int[(const int)(2 * l + 1)]; 124 visited = new boolean[(const int)(2 * l + 1)]; 125 last = new int[(const int)(2 * l + 1)]; 126 lase = new int[(const int)(2 * l + 1)]; 127 mflow = new int[(const int)(2 * l + 1)]; 128 cost = 0; 129 spfa(l, l - 1); 130 spfa(l, l - 1); 131 fout << (cost); 132 } 133 134 int main() { 135 init(); 136 solve(); 137 return 0; 138 }

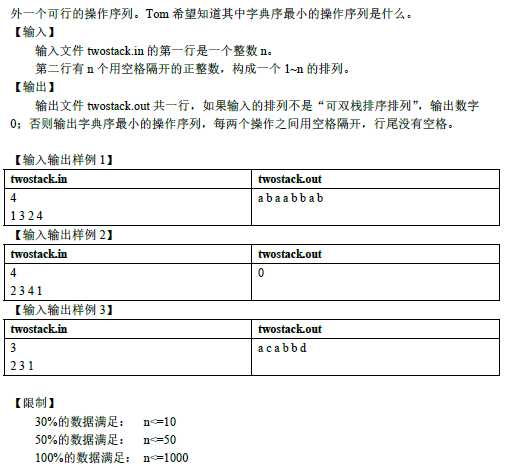
首先来思考一下,对于单栈排序的要求。
当且仅当存在这种情况不能排序:存在某个数j使得lis[j]大于它左边的某个位置i(i < j)的值lis[i],又大于右边某个位置k(k > j)的值lis[k],且lis[i]>lis[k]。可以随便举点例子2 3 1,2 4 3 1...这里就简单地说明一下,因为排序要是小的在前面,那么在k前面的都得先进栈,因为j在i后面,所以是lis[j]先被弹出栈,但lis[i]应该在它的前面,所以说这种情况不可以。
当然考虑全面点还可以考虑一下其他情况
现在回到双栈排序,对于不能用单栈排序完成的就扔到另一个栈完成...然后就会发现,这是一个二分图染色,对于有序数对(i,j)(i < j)满足上上面的情况,则就在i,j连一条边,因为i,j不能一个栈内排序,所以相连的点的颜色要不同。至于染色的方法可以参考noip2010第三题二分答案中判断的过程。
如果中间任何一个dfs的返回值为false,就说明无法用2个栈排序,按照题目意思输出0。
最后就是按照题目意思,进行一个模拟:现在要把i弹出到输出队列,如果i不在双栈中,就把它及其它前面的元素放到stack[color[j]]中,然后再把它弹出来,否则就看看在哪个栈中,然后把它弹出来。然后题目要你输出什么就怎么输出。
另外还有一个问题,建立二分图的时候如果暴力枚举i,j,k那么时间复杂度是O(n3),可以发现k被重复枚举了很多次,但是我们只需要知道对于数i,在位置j后是否存在比它小的数,于是就提前处以一个exist[i][j],这就可以把时间复杂度将为O(n2)。
(PS:此题数据很水,dfs+暗黑剪枝比这种方法快得多)
1 #include<iostream> 2 #include<fstream> 3 #include<sstream> 4 #include<cstdio> 5 #include<cctype> 6 #include<cstring> 7 #include<cstdlib> 8 #include<cmath> 9 #include<algorithm> 10 #include<queue> 11 #include<vector> 12 #include<stack> 13 #include<map> 14 #include<set> 15 using namespace std; 16 typedef bool boolean; 17 #define INF 0xfffffff 18 #define smin(a, b) a = min(a, b) 19 #define smax(a, b) a = max(a, b) 20 21 #define LOCAL 22 #ifndef LOCAL 23 #define fin cin 24 #define fout cout 25 #else 26 ifstream fin("twostack.in"); 27 ofstream fout("twostack.out"); 28 #endif 29 30 template<typename T>class Matrix{ 31 public: 32 T *p; 33 int lines; 34 int rows; 35 Matrix():p(NULL){ } 36 Matrix(int rows, int lines):lines(lines), rows(rows){ 37 p = new T[(lines * rows)]; 38 } 39 T* operator [](int pos){ 40 return (p + pos * lines); 41 } 42 }; 43 #define matset(m, i, s) memset((m).p, (i), (s) * (m).lines * (m).rows) 44 45 ///map template starts 46 typedef class Edge{ 47 public: 48 int end; 49 int next; 50 Edge(const int end = 0, const int next = 0):end(end), next(next){} 51 }Edge; 52 typedef class MapManager{ 53 public: 54 int ce; 55 int *h; 56 Edge *edge; 57 MapManager():h(NULL), edge(NULL){ } 58 MapManager(int points, int limit):ce(0){ 59 h = new int[(const int)(points + 1)]; 60 edge = new Edge[(const int)(limit + 1)]; 61 memset(h, 0, sizeof(int) * (points + 1)); 62 } 63 inline void addEdge(int from, int end){ 64 edge[++ce] = Edge(end, h[from]); 65 h[from] = ce; 66 } 67 inline void addDoubleEdge(int from, int end){ 68 addEdge(from, end); 69 addEdge(end, from); 70 } 71 Edge& operator [](int pos) { 72 return edge[pos]; 73 } 74 inline void clear() { 75 delete[] h; 76 delete[] edge; 77 } 78 }MapManager; 79 #define m_begin(g, i) (g).h[(i)] 80 ///map template ends 81 82 int n; 83 int* lis; 84 Matrix<boolean> exist; 85 MapManager g; 86 87 inline void init() { 88 fin >> n; 89 lis = new int[(const int)(n + 1)]; 90 for(int i = 1; i <= n; i++) 91 fin >> lis[i]; 92 } 93 94 inline void init_map() { 95 exist = Matrix<boolean>(n + 1, n + 2); 96 matset(exist, false, sizeof(boolean)); 97 for(int i = 1; i < n; i++) { 98 for(int j = n; j > i; j--) { 99 if(exist[i][j + 1] || lis[j] < lis[i]) 100 exist[i][j] = true; 101 } 102 } 103 104 g = MapManager(n, 2 * n * n); 105 for(int i = 1; i < n; i++) { 106 for(int j = i + 1; j <= n; j++) { 107 if(lis[j] > lis[i] && exist[i][j]) 108 g.addDoubleEdge(i, j); 109 } 110 } 111 } 112 113 int* color; 114 boolean dfs(int node, int val) { 115 if(color[node] != -1) return color[node] == val; 116 else color[node] = val; 117 for(int i = m_begin(g, node); i != 0; i = g[i].next) { 118 int& e = g[i].end; 119 if(!dfs(e, val ^ 1)) return false; 120 } 121 return true; 122 } 123 124 inline void coloring() { 125 color = new int[(const int)(n + 1)]; 126 memset(color, -1, sizeof(int) * (n + 1)); 127 for(int i = 1; i <= n; i++) { 128 if(color[i] == -1) 129 if(!dfs(i, 0)) { 130 fout << 0 << endl; 131 exit(0); 132 } 133 } 134 g.clear(); 135 delete[] exist.p; 136 } 137 138 int *s[2]; 139 int tops[2] = {0, 0}; 140 int *status; 141 char its[3] = {‘a‘, ‘c‘}; 142 inline void solve() { 143 for(int i = 0; i < 2; i++) 144 s[i] = new int[(const int)(n + 1)]; 145 status = new int[(const int)(n + 1)]; 146 memset(status, -1, sizeof(int) * (n + 1)); 147 for(int i = 1, j = 1; i <= n; i++) { 148 if(status[i] == -1) { 149 while(j <= n && lis[j] != i) { 150 s[color[j]][tops[color[j]]++] = lis[j]; 151 status[lis[j]] = color[j]; 152 fout << its[color[j]] << " "; 153 j++; 154 } 155 status[lis[j]] = color[j]; 156 fout << its[color[j]] << " " << (char) (its[color[j]] + 1) << " "; 157 j++; 158 } else { 159 --tops[status[i]]; 160 fout << (char) (its[status[i]] + 1) << " "; 161 } 162 } 163 #ifdef LOCAL 164 fin.close(); 165 fout.close(); 166 #endif 167 } 168 169 int main() { 170 init(); 171 init_map(); 172 coloring(); 173 solve(); 174 return 0; 175 }
标签:matrix img ddd ifstream std visit 模拟 fst stack
原文地址:http://www.cnblogs.com/yyf0309/p/6442265.html