标签:之间 约数 并且 问题: 设计 编程 答案 算法 等于
一、题目
小易是一个数论爱好者,并且对于一个数的奇数约数十分感兴趣。一天小易遇到这样一个问题: 定义函数f(x)为x最大的奇数约数,x为正整数。 例如:f(44) = 11.
输入一个整数N (1 ≤ N ≤ 1000000000)
输出一个整数,即为f(1) + f(2) + f(3).......f(N)
7
21
二、答案解析
刚读完题,小编马上就有了思路,还有点小得意,写完之后,然后进行了代码测试,谁曾想,算法因为时间复杂度太大,不能通过测试,当然是不合格喽。
以下是不合格的算法,思路很单纯,就是从1到n循环,每次循环求出当前数的最大奇约数,然后累加,这个算法在小编的电脑上(2016的13英寸MAC中配)输入了1,000,000,000,然后用了39657ms计算完毕,晕的一逼,算法写成这样也是没谁了
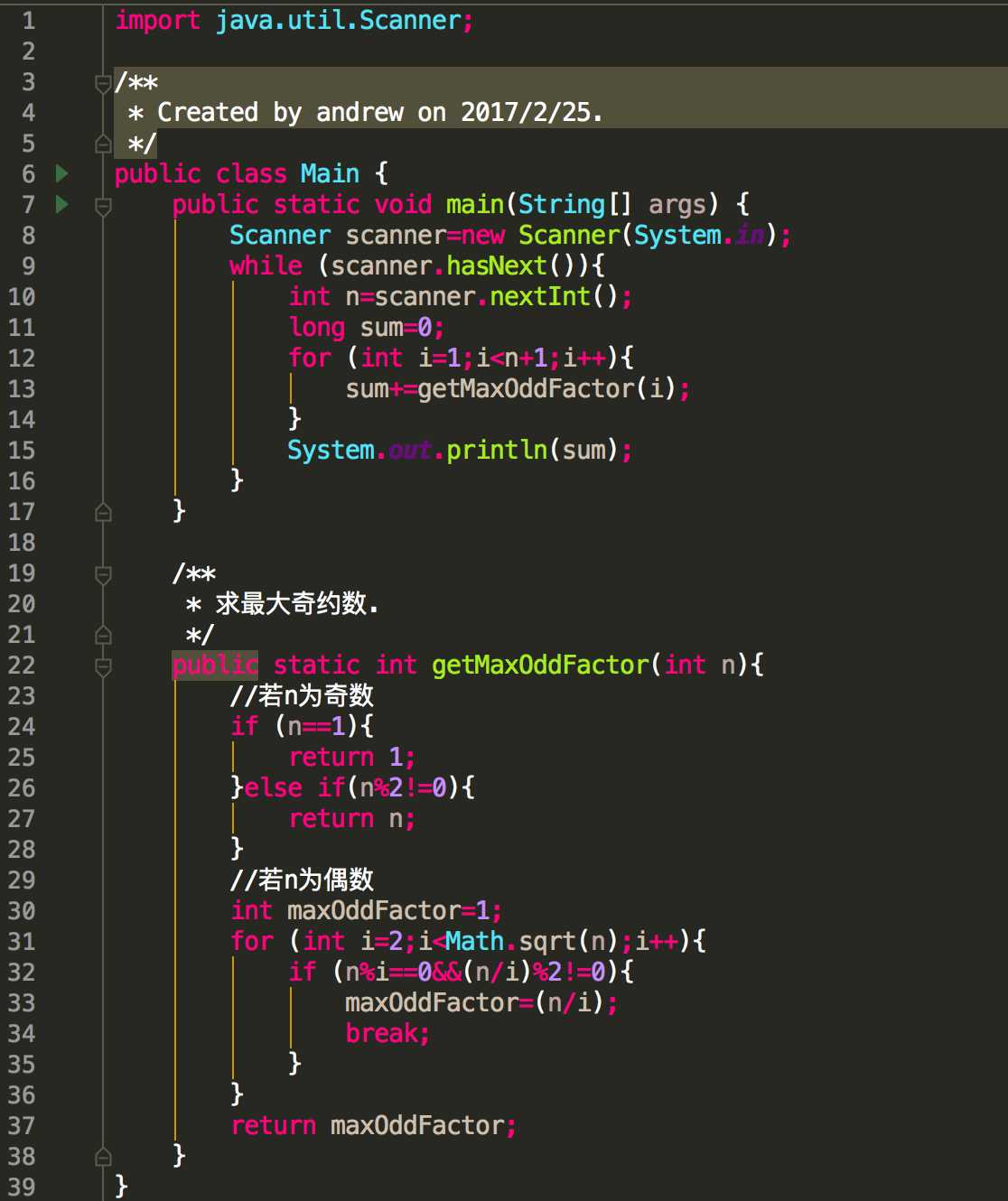
—————————————华丽的分割线———————————
正确的姿势是这样的:
首先,先讨论一下数的奇约数,奇数的最大奇约数就是本身,偶数要不断地除以2,直到除以2的结果是奇数,那么这个结果就是其最大奇约数
在看我们的题目要求,是求出从1到n之间(包括1和n)的每个数的最大奇约数,然后对它们求和。
1.当n是奇数时,那么在1到n之间共有(n+1)/2个奇数,根据等差数列求和的理论,sn=(首项+末项)*项数/2,这些奇数的和为(n+1)/2*(n+1)/2;
2.当n是偶数时,那么在1到n之间共有n/2个奇数,这些奇数的和为n/2*n/2,当然在Java中也可以表示为:(n+1)/2*(n+1)/2;
然后这些只是范围内所有奇数的最大奇约数之和,那么剩余的偶数的奇约数之和怎么求呢,是这样的:
我们可以让n除以2,然后求出1到n/2范围内的所有奇数的最大奇约数之和,与之前的求和进行累加,如此让n不断地除以2,直到等于0,那么这所有的累加就是要求的数。
算法的实现如下:
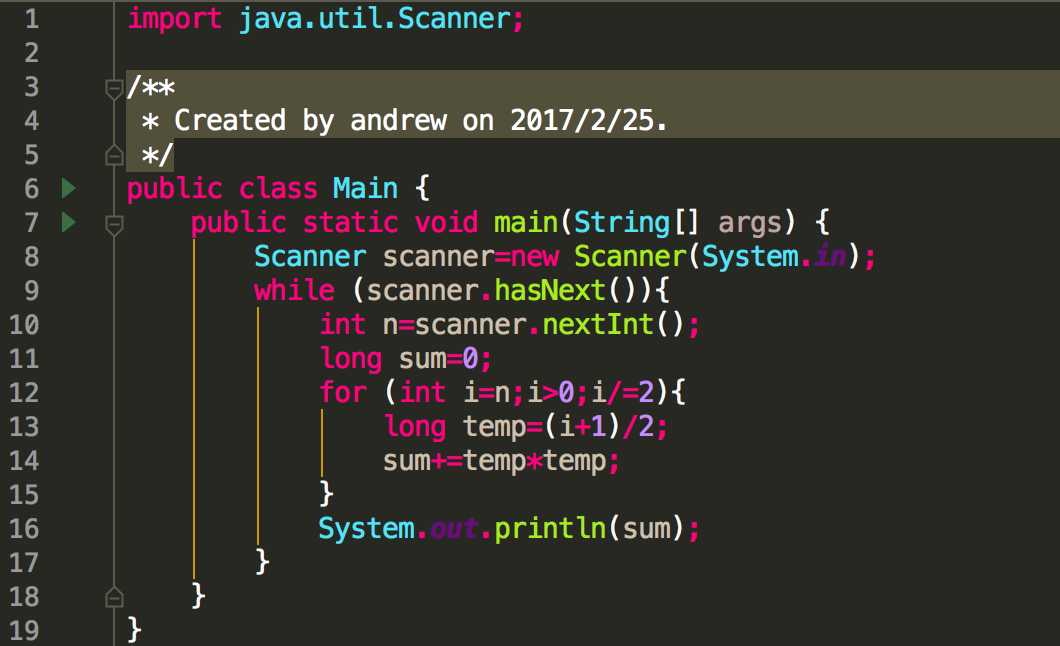
标签:之间 约数 并且 问题: 设计 编程 答案 算法 等于
原文地址:http://www.cnblogs.com/JSONBEAN/p/6442537.html