标签：模型   传递   font   边界条件   单位   数学模型   ges   读书   分享   

1.3时间域描述

1.3.1

微分方程用来描述物理传递环节和系统的数学模型。

微分方程可以在一直输入量和边界条件的情况下计算出有关的输出量。

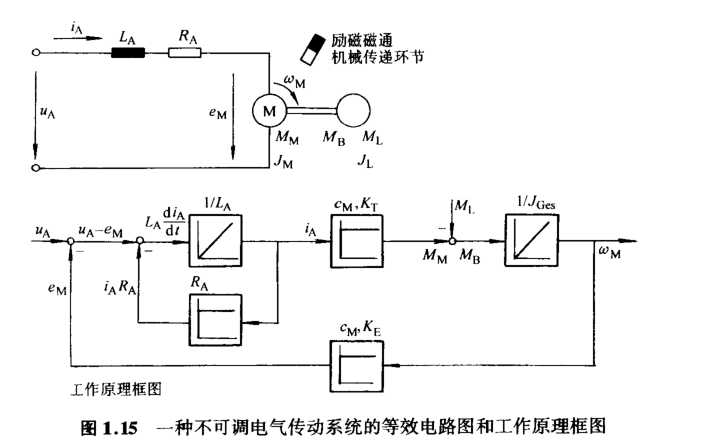
首先概括出物理规律性，然后建立起工作原理框图，推导出不可调传动系统的微分方程。

经过一系列的变换就可以得到不可调电气传动系统的二阶微分方程。

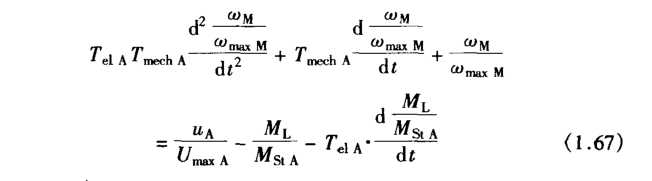
假定ML = 0，就可以解微分方程确定输出电压变化时的基准相应特性。

阶跃响应特性：

用来描述一个传递环节或一个系统的输出量在输入量发生一次阶跃式变化时的随时间变化过程。 可用来调节技术特性，

将微分方程简化：

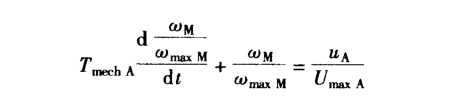
在线性系统情况下。齐次的部分解描述系统动态部分，而特解则描述静止状态。两部分解之和就产生总解。

齐次部分解可以求出

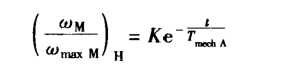
非齐次的部分解：

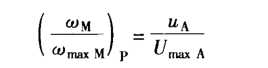
则微分方程的解为：

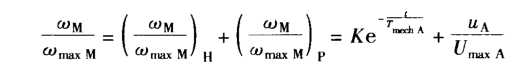
进而得出

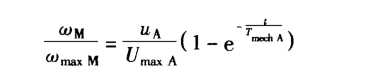
可以看出，一个不可调传动系统的角速度Wm或转速Nm,在阶跃式接入电枢电压ua之后，按带有机械时间常数TmechA的指数函数形式变化。（前提无负载启动、电气时间常数TelA可忽略）

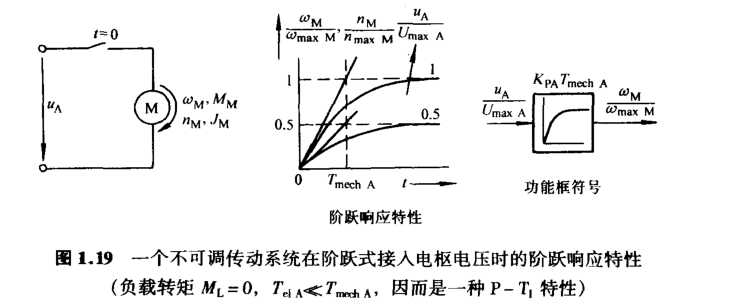
除了阶跃函数之外，还有另外两种在时间域中描述传递环节特性的方法。上升斜坡响应特性和单位脉冲响应特性，这些方法在传动技术中没有多大意义。

自动化技术中的进给电气传动-读书笔记3

标签：模型   传递   font   边界条件   单位   数学模型   ges   读书   分享   

原文地址：http://www.cnblogs.com/koumeng/p/6443954.html