标签:target tags int ott http math size pad 次方
梯度下降(Gradient Descent)是最基础的优化算法。在微积分中,梯度表示函数增长速度最快的方向。在机器学习问题中,我们的目标常常是求极大值或者极小值。梯度下降法就是沿着梯度的不断走的方法,当求极小值时沿与梯度相反的方向
用通俗的话说,梯度下降法就像下山,我们会沿着当前最快下降的道路走,直至走至山底(当然这条路未必是最快到达山底的)。
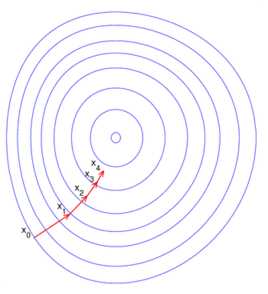
如图,在一个求极小值的问题中,我们会沿着梯度不断往下走,直至走至一个最低点(局部最优)。
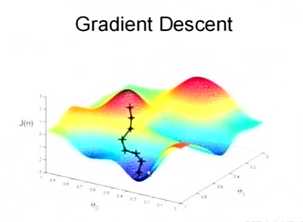
先从简单的一元二次方程开始说起。我们拥有一个函数, ,他的导数就是
,他的导数就是 。而对于大部分函数而言它的梯度就是它的负导数。
。而对于大部分函数而言它的梯度就是它的负导数。
我们使用matplotlib画出这个函数的图
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-5,3,20)
y = x**2+2*x+1
plt.plot(x,y)
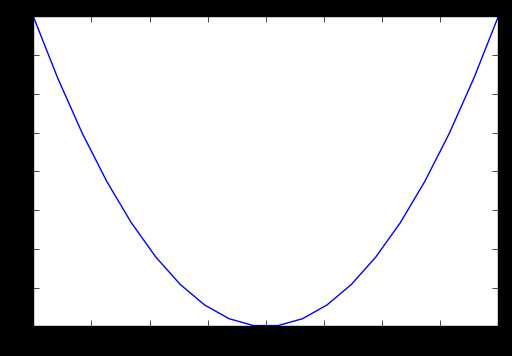
目标函数以及它的导数
f = lambda x:x**2+2*x+1
g = lambda x: 2*x+2
梯度下降法的python表示
def gd(x_start,step,g,itera):
#x_start 起始点
#step 步长
#g 梯度
#itera 迭代次数
x = x_start
for i in range(itera):
grad = g(x)
x -= grad*step
print("Epoch{0}:grad={1},x={2}".format(i,grad,x))
if abs(grad)<1e-6:
break
return x
Epoch29:grad=0.01856910058928074,x=-0.9925723597642877
最终答案离-1的举例已经很小了
当我们把step的值使用1.1代入时,迭代次数不变会怎么样呢?
>>>gd(5,1.1,g,30)
Epoch29:grad=-2373.7631379977083,x=1423.2578827986254
你会发现x会离目标越来越远
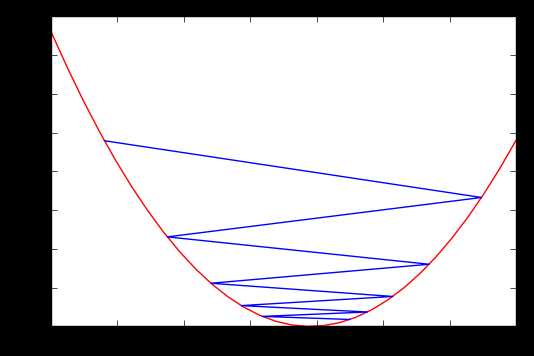
当我们的step值使用0.0001代入时,迭代次数不变时的答案又是怎么样的呢
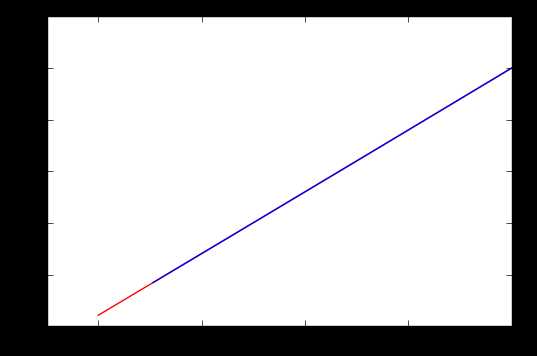
你会发现他虽然沿着梯度不断向下走但在总体看来几乎没怎么变·
当你把迭代次数增加到一定大时,它仍然能达到最低点。
当步长过长时,有可能会使梯度下降法无法收敛。
当步长小时,适当增加迭代次数,仍能达到最优解。但是过多的迭代次数会增加训练的时间。
标签:target tags int ott http math size pad 次方
原文地址:http://www.cnblogs.com/lynsyklate/p/6444053.html