略谈矩阵乘法优化递推

标签：次方   for   结构   例题   idt   size   display   简单   tin   

1、矩阵基本概念：

矩阵大概就是二维数组存储的样子，然后每一个地方都有元素。

例如：

然后是矩阵的乘法：

矩阵的了解就到这里了

2、引入

　求斐波那契数列第n项，n<=10^9.

　　1、通项公式：

　　　　

　　　　不足：

　　　　　　要求n次方。

　　　　　　虽说n次方可以log2出解，但是精度问题值得考量。

　　2、矩阵快速幂：

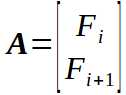
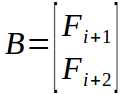
　　　　先在考虑将A矩阵转化成B矩阵。

　　　　发现有这样一个转移矩阵。

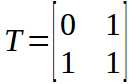
　　　　使得

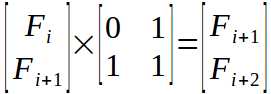
　　　　所以我们可以用矩阵解决了。即：

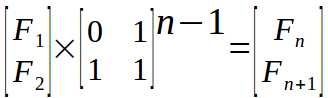
 　　　  不过单纯这么用矩阵显然是远远不够的，因为一步一步是O(n)的，因此我们要用快速幂，如下伪代码：

1 Matrix A,C;//定义矩阵(Matrix 用结构体实现)
2 for(;n;n>>=1,C*=C)
3     if(n&1)
4         A*=C;
5 print(A);

//不要复制这一段，是伪代码！！！

3、转移矩阵的简单推导

4、例题(待添加)

略谈矩阵乘法优化递推

标签：次方   for   结构   例题   idt   size   display   简单   tin   

原文地址：http://www.cnblogs.com/Never-See/p/6445019.html