标签:matrix 数据 rtl 汉明码 需要 输入 http mode 讲解
此文章为原创出自 V3学院 www.v3edu.org,FPGA培训专家
汉明码是一种实现简单并且可以检测和纠正错误的编码, 汉明码是在原编码的基础上附加一部分数据比特,使其满足纠错码的条件。它属于线性分组码,由于线性码的编码和译码容易实现,至今仍是应用最广泛的一类码。
V3学院FPGA Verilog 汉明码实现,Hamming(12,8)表示数据位长K=8,编码后码字长N=12,校验位长R=12-8=4,最小汉明距离是H=3(观察其生成矩阵,不同行向量间最少不同比特的数量),纠错能力为(H-1)/2=2/2=1.
Hamming(12,8)生成矩阵为:
表 2.2 Hamming(12,8) 生成矩阵
标号 11 10 9 8 7 6 5 4 3 2 1 0
编号 X^7 X^6 X^5 X^4 X^3 X^2 X^1 1 C3 C2 C1 C0
1 1 0 0 0 0 0 0 0 1 1 1 0
2 0 1 0 0 0 0 0 0 0 1 1 1
3 0 0 1 0 0 0 0 0 1 0 1 0
4 0 0 0 1 0 0 0 0 0 1 0 1
5 0 0 0 0 1 0 0 0 1 0 1 1
6 0 0 0 0 0 1 0 0 1 1 0 0
7 0 0 0 0 0 0 1 0 0 1 1 0
8 0 0 0 0 0 0 0 1 0 0 1 1
注:X^n表示X的n次方,例如8’b00010001,从右边数第0位和第4位为1,那么多项式表示就是X^4+X^0=X^4+1
2.2.1编码过程:
设:表2.2中的生成矩阵表示为G,待编码数据表示为A,G是8行12列的矩阵,A是位宽为8的向量,编码后数据为12bit向量B。
B=GxA (此乘法为矩阵乘)
B[11]=A[7]
B[10]=A[6]
B[9]=A[5]
B[8]=A[4]
B[7]=A[3]
B[6]=A[2]
B[5]=A[1]
B[4]=A[0]
B[3]=A[7]+A[5]+A[3]+A[2]
B[2]=A[7]+A[6]+A[4]+A[2]+A[1]
B[1]=A[7]+A[6]+A[5]+A[3]+A[1]+A[0]
B[0]=A[6]+A[4]+A[3]+A[0]
注:方括号中的数字是数据比特的下标。其中+号为异或逻辑运算。
2.2.2编码过程的RTL代码实现:
//汉明码编码模块 V3学院开放源码
//目的:功能模块
module hamming_12_8(
input wire sclk,
input wire rst_n,
input wire data_inv,//待编码数据有效标志
input wire [7:0] data_in, ,//待编码数据
output reg data_ov,//编码后数据有效标志
output reg [11:0] data_o,//编码后数据
output wire tout//测试接口
);
/*********************************************\
生成矩阵
Hamming 12 8 generator matrix G(X)={In-k P}
1 0 0 0 0 0 0 0 1 1 1 0
0 1 0 0 0 0 0 0 0 1 1 1
0 0 1 0 0 0 0 0 1 0 1 0
0 0 0 1 0 0 0 0 0 1 0 1
0 0 0 0 1 0 0 0 1 0 1 1
0 0 0 0 0 1 0 0 1 1 0 0
0 0 0 0 0 0 1 0 0 1 1 0
0 0 0 0 0 0 0 1 0 0 1 1
b=data_inG
********************************************/
always @(posedge sclk or negedge rst_n)
if(rst_n==1‘b0)
data_o<=‘d0;
else if(data_inv==1‘b1)
data_o<={data_in,
data_in[7]^data_in[5]^data_in[3]^data_in[2],
data_in[7]^data_in[6]^data_in[4]^data_in[2]^data_in[1],
data_in[7]^data_in[6]^data_in[5]^data_in[3]^data_in[1]^data_in[0],
data_in[6]^data_in[4]^data_in[3]^data_in[0]
};
always @(posedge sclk or negedge rst_n)
if(rst_n==1‘b0)
data_ov<=‘d0;
else if(data_inv==1‘b1)
data_ov<=1‘b1;
else data_ov<=1‘b0;
endmodule
2.2.3解码过程
在表2.2中生成矩阵G是由单位矩阵I和矩阵P组成,其中0至3列为4x8的矩阵P,其余的是8x8的矩阵I。
解码首先需要校验矩阵H,校验矩阵H是表示为{P^t,I(N-K)},P^t表示矩阵P的转置,I(N-K)其中N=12,K=8,那么I(4)表示的是4x4的单位矩阵。
表2.3 Hamming(12,8) 校验矩阵
标号 11 10 9 8 7 6 5 4 3 2 1 0
矩阵 P^t I(N-K)
1 1 0 1 0 1 1 0 0 1 0 0 0
2 1 1 0 1 0 1 1 0 0 1 0 0
3 1 1 1 0 1 0 1 1 0 0 1 0
4 0 1 0 1 1 0 0 1 0 0 0 1
得到校验矩阵H之后,通过校验矩阵求得校正子,S=H^txU,其中U表示待解码的12bit向量,H^t是校验矩阵的转置。
S[3]= U[11]+ U [9]+ U[7]+U[6]+U[3];
S[2]=U[11]+U[10]+U[8]+U[6]+U[5]+U[2];
S[1]=U[11]+U[10]+U[9]+U[7]+U[5]+U[4]+U[1];
S[0]=U[10]+U[8]+U[7]+U[4]+U[0];
注:方括号内为向量的比特下标,加号为异或运算。
通过错误模式求校正子矩阵,汉明码只能校正1bit错误,那么包括没有错误的情况一共有13中情况,错误模式矩阵为E,校正子矩阵为S,校验矩阵为H,他们的关系为S=H^tE;
S(i)=H^tE(i);
i是矩阵的行向量下标
E(i) S(i) 错误模式矩阵E(MSB TO LSB) 校验矩阵的转置H^t 校正子矩阵S
E(12) 0000_0000_0000 0000
1110
0111
1010
0101
1011
1100
0110
0011
1000
0100
0010
0001 0000
E(11) 1000_0000_0000 1110
E(10) 0100_0000_0000 0111
E(9) 0010_0000_0000 1010
E(8) 0001_0000_0000 0101
E(7) 0000_1000_0000 1011
E(6) 0000_0100_0000 1100
E(5) 0000_0010_0000 0110
E(4) 0000_0001_0000 0011
E(3) 0000_0000_1000 1000
E(2) 0000_0000_0100 0100
E(1) 0000_0000_0010 0010
E(0) 0000_0000_0001 0001
通过以上推到,如果校正子S(12)=0000,那么证明没有数据比特错误。以此类推S(11)=1110证明输入向量U的第11比特出错也就是U[11]错误了,因此把U[11]取反即可校正错误,按照此方法即可实现汉明码的译码。可以写为U[11]=U[11]+(S[3]&S[2]&S[1]&~S[0]),这里S[n]为校正子的比特下标,如果校正子里S[n]为1则取反,用意是如果校正子匹配S正确则U[11]比特取反,如果匹配S错误则认为不存在错误保持U[11]不变。 U[11]=U[11]+(S[3]&S[2]&S[1]&~S[0])
U[10]=U[10]+( ~S[3]&S[2]&S[1]&S[0]) U[09]=U[09]+( S[3]&~S[2]&S[1]&~S[0])
U[08]=U[08]+( ~S[3]&S[2]&~S[1]&S[0]) U[07]=U[07]+( S[3]&~S[2]&S[1]&S[0])
U[06]=U[06]+( ~S[3]&~S[2]&S[1]&S[0]) U[05]=U[05]+( ~S[3]&S[2]&S[1]&~S[0])
U[04]=U[04]+( ~S[3]&~S[2]&S[1]&S[0]) U[03]=U[03]+( S[3]&~S[2]&~S[1]&~S[0])
U[02]=U[02]+( ~S[3]&S[2]&~S[1]&~S[0]) U[01]=U[01]+(~ S[3]&~S[2]&S[1]&~S[0])
U[00]`=U[00]+( ~S[3]&~S[2]&~S[1]&S[0])
注:方括号内为向量的比特下标,加号为异或运算。
2.2.4 V3学院FPGA Verilog 汉明码实现编码过程的RTL代码实现:
//汉明码解码模块
//目的:功能模块
module dehamming_12_8(
input wire sclk,
input wire rst_n,
input wire data_inv,//待解码数据有效标志
input wire [11:0] data_in,//待解码数据
output reg data_ov,//解码后数据有效标志
output reg [11:0] data_o,//解码后数据
output wire tout//测试接口
);
/********************************************************\
校验矩阵H={P^t In-k}
1 0 1 0 1 1 0 0 1 0 0 0
1 1 0 1 0 1 1 0 0 1 0 0
1 1 1 0 1 0 1 1 0 0 1 0
0 1 0 1 1 0 0 1 0 0 0 1
s[=H^T*data_in
********************************************************/
wire [3:0] s;
wire [11:0] e;
assign s[3]=data_in[11]^data_in[9]^data_in[7]^data_in[6]^data_in[3];
assign s[2]=data_in[11]^data_in[10]^data_in[8]^data_in[6]^data_in[5]^data_in[2];
assign s[1]=data_in[11]^data_in[10]^data_in[9]^data_in[7]^data_in[5]^data_in[4]^data_in[1];
assign s[0]=data_in[10]^data_in[8]^data_in[7]^data_in[4]^data_in[0];
assign e[11]=s[3]&s[2]&s[1]&(~s[0]);
assign e[10]=(~s[3])&s[2]&s[1]&s[0];
assign e[9] =s[3]&(~s[2])&s[1]&(~s[0]);
assign e[8] =(~s[3])&s[2]&(~s[1])&s[0];
assign e[7] =s[3]&(~s[2])&s[1]&s[0];
assign e[6] =s[3]&s[2]&(~s[1])&(~s[0]);
assign e[5] =(~s[3])&s[2]&s[1]&(~s[0]);
assign e[4] =(~s[3])&(~s[2])&s[1]&s[0];
assign e[3] =s[3]&(~s[2])&(~s[1])&(~s[0]);
assign e[2] =(~s[3])&s[2]&(~s[1])&(~s[0]);
assign e[1] =(~s[3])&(~s[2])&s[1]&(~s[0]);
assign e[0] =(~s[3])&(~s[2])&(~s[1])&s[0];
always @(posedge sclk or negedge rst_n)
if(rst_n==1‘b0)
data_o<=‘d0;
else if(data_inv==1‘b1)
data_o<={data_in[11]^e[11],data_in[10]^e[10],
data_in[9]^e[9],data_in[8]^e[8],
data_in[7]^e[7],data_in[6]^e[6],
data_in[5]^e[5],data_in[4]^e[4],
data_in[3]^e[3],data_in[2]^e[2],
data_in[1]^e[1],data_in[0]^e[0]};
always @(posedge sclk or negedge rst_n)
if(rst_n==1‘b0)
data_ov<=‘d0;
else if(data_inv==1‘b1)
data_ov<=‘d1;
else
data_ov<=‘d0;
endmodule
2.2.5 Testbench激励:(下一篇中继续讲解modelsim仿真过程,请持续关注V3学院FPGA Verilog)
为了测试汉明编码和解码模块的功能正确性编写了如下模块,逻辑架构见图2.1:
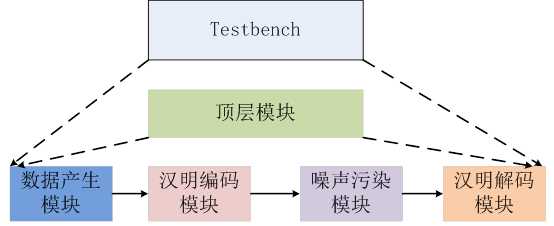
V3学院带你学习-缩短汉明码Hamming(12,8)的FPGA实现
标签:matrix 数据 rtl 汉明码 需要 输入 http mode 讲解
原文地址:http://www.cnblogs.com/Y---L----/p/6473104.html