标签:解析 利用 技术分享 允许 ima 微分方程 电气 静态 png
知识要点:
1.3 时间域描述
1.3.1 微分方程
对于各有一个输入端和输出端的线性传递环节来说,如果是一个时间和数值连续的输入量u(t),那么,输出量v(t)就有下列一般形式的微分方程
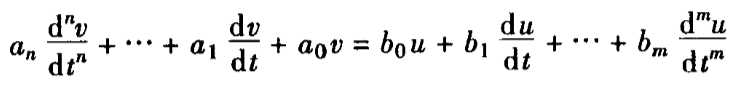
在大多数情况下很难采用微分方程进行计算。在实际中,利用这些微分方程来从物理定律中推导出传递环节的特性。
静态传递特性以及动态传递特性解析法描述的基础是与下图相一致的不可调传动系统的等效电路图。
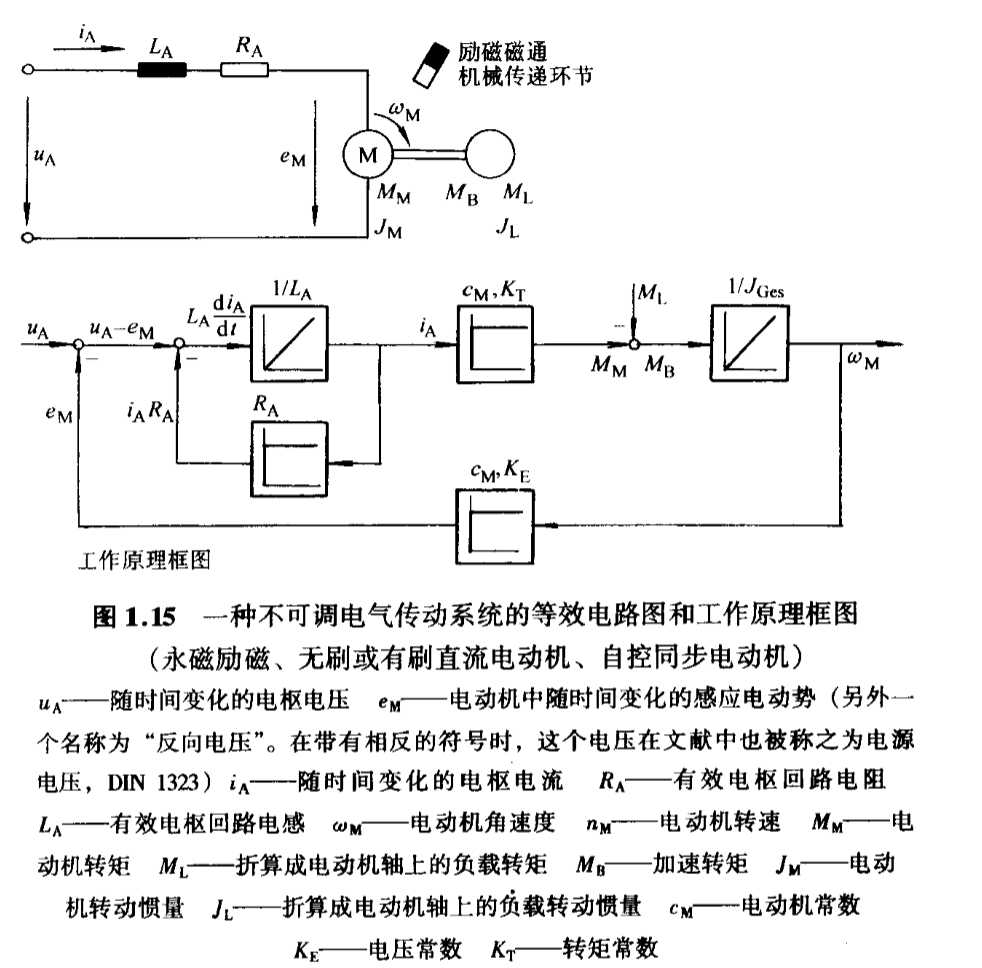
在不可调传动系统情况下,在系统稳定状态下,一个接入的负载转矩会产生一个角速度的固定偏差。为找出起始特性,研究t=0这个瞬间时刻负载转矩的跃变。
n=m:当出现一个输入量跃变时,输出量也同样出现一个跃变。
n=m+1:当出现一个输入量跃变时,输出量表现出一个有限的上升速度。
n=m+k(k>=2):当出现一个输入量跃变时,输出量没有出现随时间变化,其初始切线呈水平变化。
(n是输出量的微分阶段,m是输入量的微分阶段)。
1.3.2 阶跃响应特性
将不可调电气系统的二阶微分方程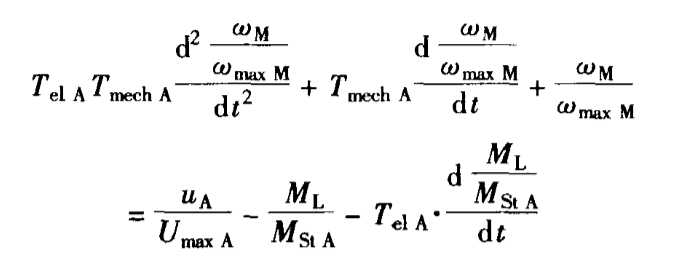
简化为: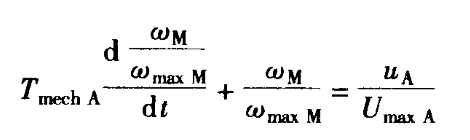
在线性系统情况下,以齐次和非齐次的部分解(特解)为根据。齐次部分解描述系统的动态部分,特解描述静止状态。两部分解之和产生出总解。
齐次的部分解: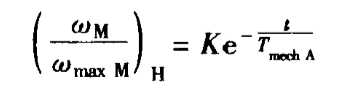
非齐次的部分解: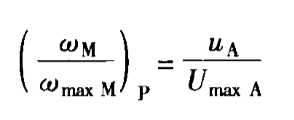
由齐次和非齐次的解(特解)之和得出微分方程的解为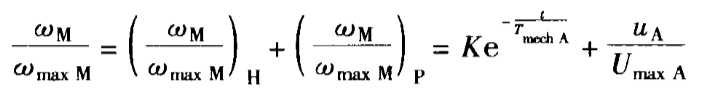
设定:t=0和wM=0,得出K值: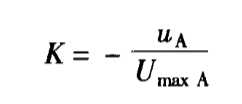
微分方程的解为: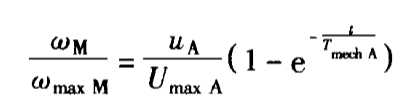
可得出如下结论:
一个不可调传动系统的角速度和转速,在阶跃式接入电枢电压uA之后,按带有机械时间常数Tmech A的指数函数(简称e函数)的形式变化。其前提条件是:无负载起动(ML=0),电气时间常数Tel A可以忽略。
上升斜坡响应特性:在传递环节的输入端施加一个斜坡函数信号,并观测输出信号的变化过程。
单位脉冲响应特性:给有待研究的传递环节加上一个脉冲输入信号。这种测试信号被应用在稳定状态中只允许小偏差的系统中,也可以适当地用它来测试单纯的积分环节。
正弦响应特性:是一个传递环节对一个正弦形频率可变输入信号的反应。
理解难点:
关于齐次和非齐次求解的具体过程不太了解。
PLECS模型:
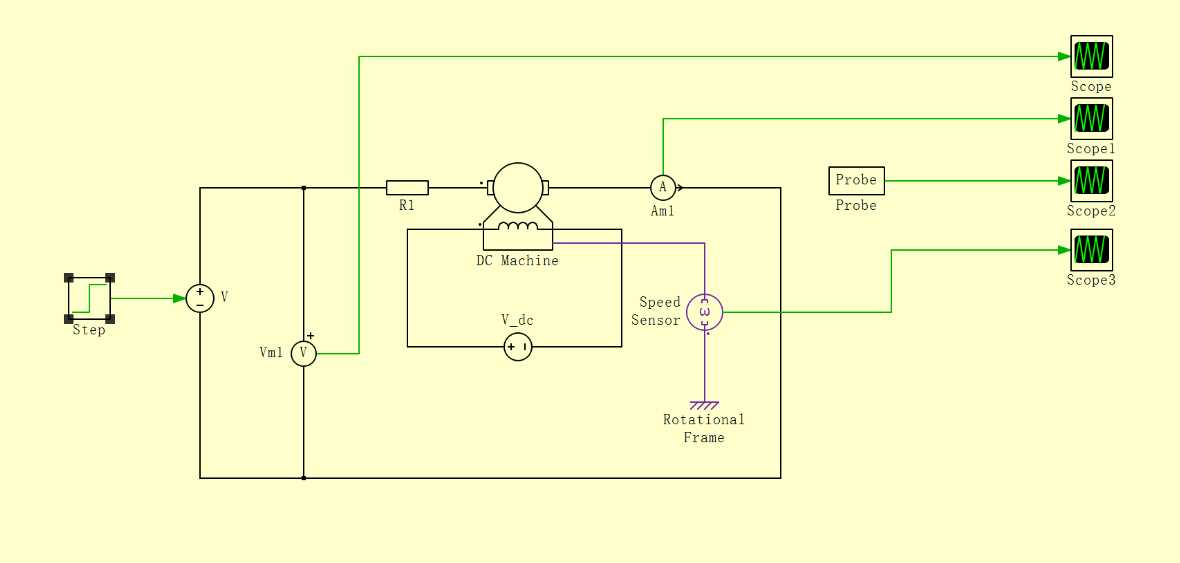
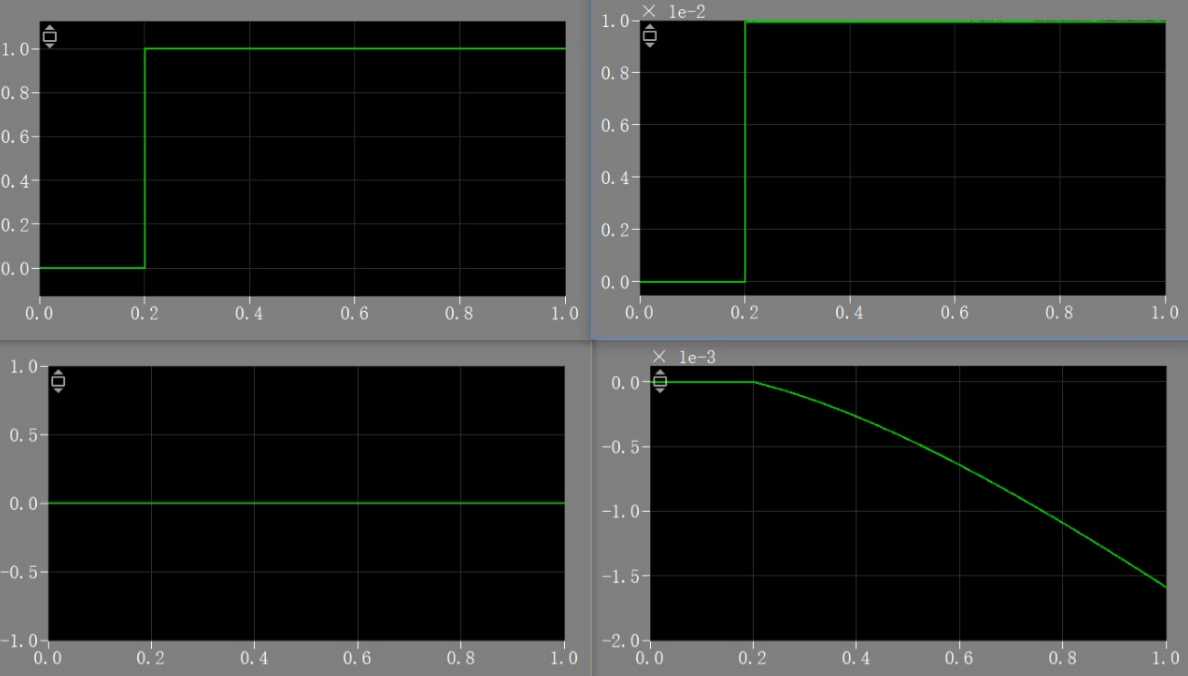
仿真结果:(由左至右,由上至下分别为Scope,Scope1,Scope2,Scope3)
(1)V=120V,R1=100Ω
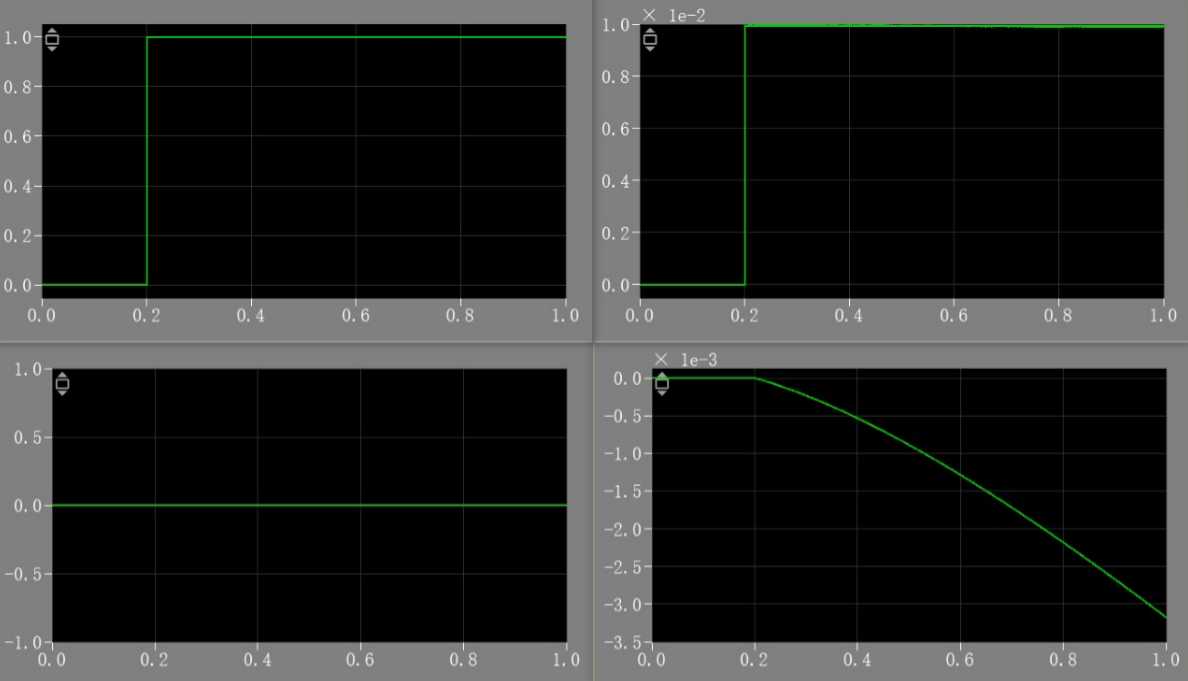
(2)V=120V,R1=10Ω
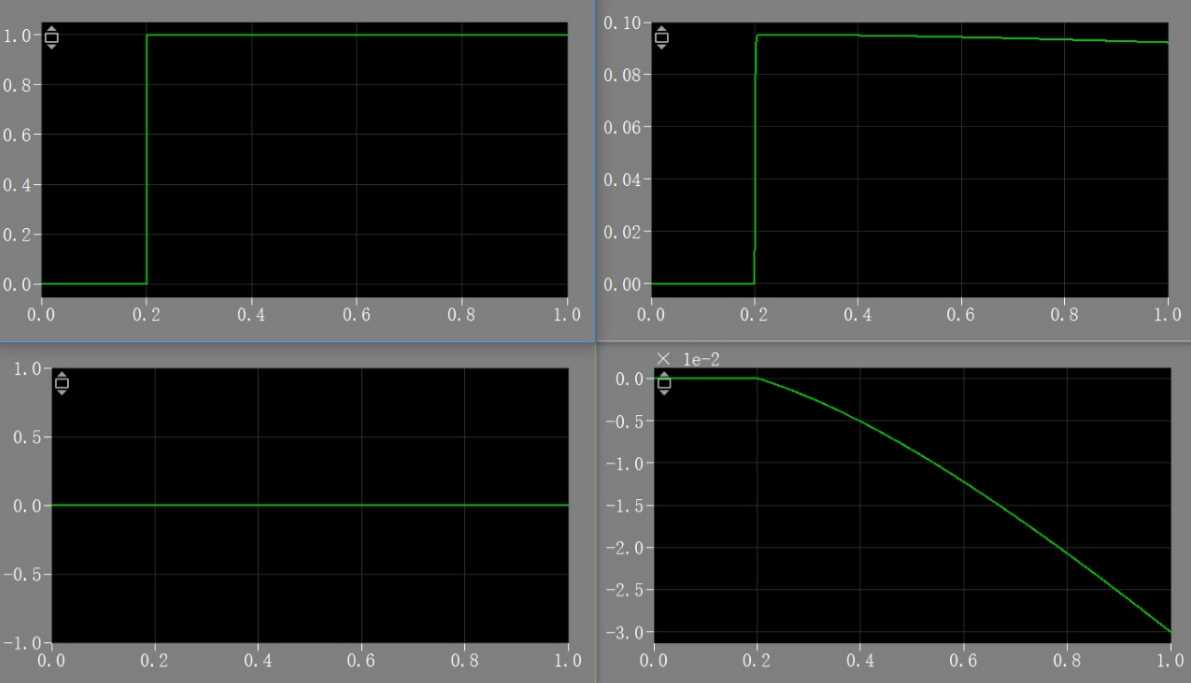
(3)V=60V,R1=100Ω
标签:解析 利用 技术分享 允许 ima 微分方程 电气 静态 png
原文地址:http://www.cnblogs.com/Tunever/p/6473227.html