标签:时间 信号 系统 技术分享 导数 速度 正弦 .com 数学模型
1.3时间域描述
微分方程:描述物理传递环节和系统的数学模型,可利用其在已知输入量和边界条件的情况下计算出有关的输出量。
选择不可调电气传动系统作为一个系统的微分方程计算实例。
等效电路图为
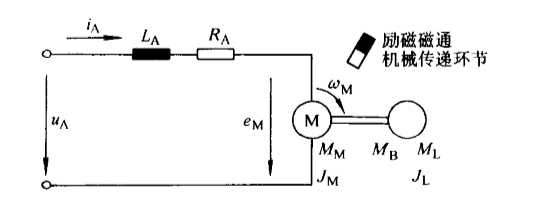
前提是,(1)将变流器装置和供电电网中的阻抗归并到电枢回路电阻RA和电枢回路电感LA上;(2)负载转矩惯量JL包括机械传递环节所有运动部件折算成电动机轴上的转动惯量;(3)励磁磁通量是时间恒定的。
电动机角速度: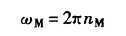
折算后的电动机轴上的总转动惯量: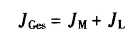
恒定磁场励磁时,直流电动机的基本方程为
电压: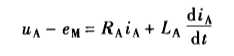 描述为反馈积分环节,或比例系数为
描述为反馈积分环节,或比例系数为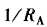 ,电气时间常数为
,电气时间常数为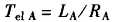 的环节。
的环节。
感应反向电压: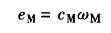 ,
,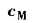 是电动机常数
是电动机常数
转矩平衡方程: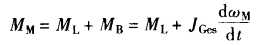
电动机转矩: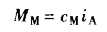
加速度转矩: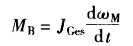
由以上关系式可得到工作原理框图:
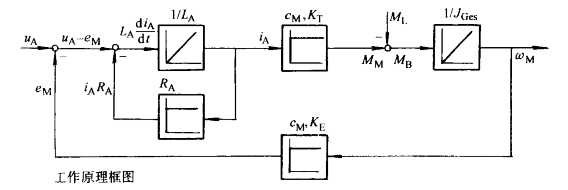
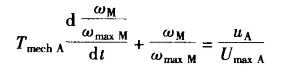
同时可推导出不可调传动系统的微分方程:
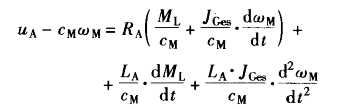
引入传动系统电气时间常数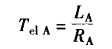
并将该方程的量值进行定标,作少许变换后就可以得到不可调电气传动系统的二阶微分方程:
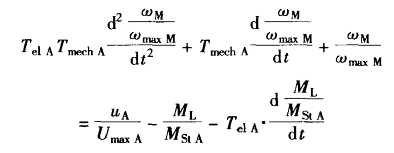
通过系数比较,特征值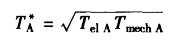
阻尼系数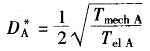 ,决定着超调量和起振时间
,决定着超调量和起振时间
将所有时间导数都设为0,得到:
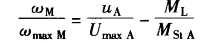
结论:
(1) 当出现一个输入量跃变时,输出量也同样出现一个跃变;
当出现一个输入量跃变时,输出量也同样出现一个跃变;
(2) 当出现一个输入量跃变时,输出量表现出一个有限的上升速度;
当出现一个输入量跃变时,输出量表现出一个有限的上升速度;
(3)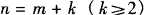 出现一个输入量跃变时,输出量没有出现随时间变化,其起始切线呈水平变化。
出现一个输入量跃变时,输出量没有出现随时间变化,其起始切线呈水平变化。
(n是输出量的微分阶数,m是输入量的微分阶数)
阶跃响应特性:描述一个传递环节或一个系统的输出量在输入量发生一次阶跃变化时的随时间变化过程。
过度函数:把输出信号的变化与输入信号的跃变高度联系在一起。
假定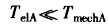 ,负载转矩
,负载转矩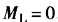 ,则微分方程简化成
,则微分方程简化成
齐次的部分解:描述动态部分
非齐次的部分解:描述静止状态
得到结论:一个不可调传动系统的角速度,在阶跃式接入电枢电压后,按带有机械时间常数的指数函数的形式变化。前提条件是:无负载启动、电气时间常数可以忽略。
上升斜坡响应特性、单位脉冲响应特性、正弦响应特性也可作为描述传递特性的方法。
标签:时间 信号 系统 技术分享 导数 速度 正弦 .com 数学模型
原文地址:http://www.cnblogs.com/darle/p/6473225.html