标签:cto for strong 合并 image sort函数 选择排序 排序 一段
本周学习分治法,故特意挑选了相关习题巩固一下,并回顾一下分治法的思路
题目:Kth Largest Element in an Array
Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element.
For example,
Given [3,2,1,5,6,4] and k = 2, return 5.
题解:
这道题要求从一串未经排序的数组中找出第K大的数,最简单的方法就是先对这串数组进行一个排序,然后输出第k大的数即可。
对数组的排序有很多算法,冒泡排序、选择排序、快速排序等等,对算法的选择不同,其相应的空间复杂度和时间复杂度也不同。因此,也复习巩固一下各类排序算法的时间、空间复杂度。
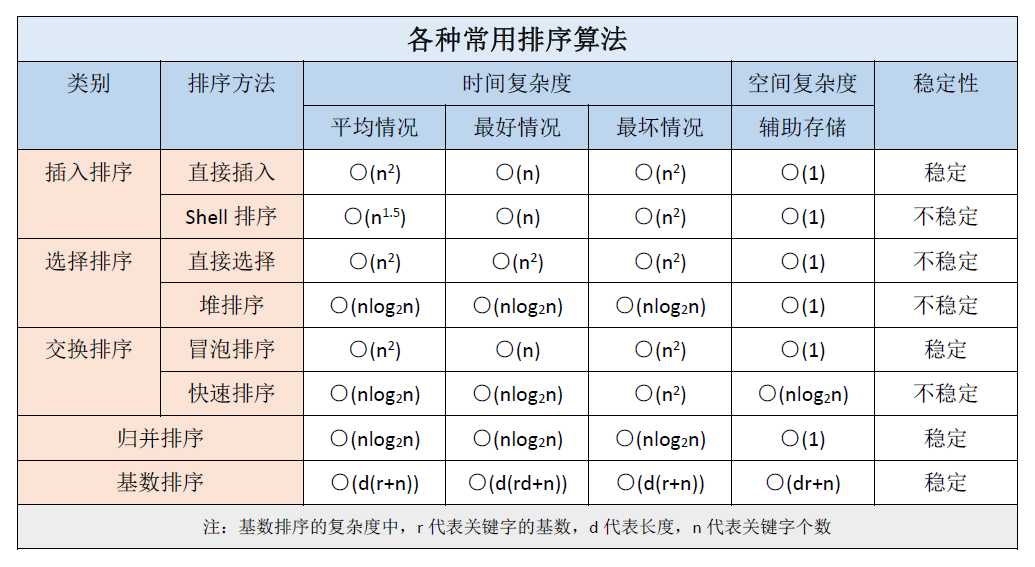
从空间复杂度和时间复杂度综合考虑,我选择了用快速排序。快速排序也是用到了分治法,将一个长的序列层层划分为若干个小序列排序,最后合并在一起。可以用递归实现。
即:用一个分区函数,对数列中的第一个数num为参考,比num小的数排在num的左边,比num大的数排在num的右边。得到两段新的乱序序列,而这两段序列相对num有序。
再用一个quicksort函数进行递归,对每一段乱序序列都进行分区,得到两段更小的乱序序列,直到只剩下一个数为止。这样下来,当递归结束后,我们就得到了一个有序的序列,将第K大的数输出即可。
上面是用快速排序的思路解这道题,但是这个题解方法还有可以优化的余地。注意题目要求的是找出第K大的数,即我们不需要将整个数列都排序完毕,只需要将第K大的数找出来就可以了。那么在使用快速排序的时候,其实我们不需要将分区函数得到的所有小段序列都进行排序。先观察快速排序的特点,每一次调用分区函数的时候,都可以得到一个有确定位置的数及其下标。那么,我们可以根据得到确定的这个数,与K相比较,只需将包含第K大的那段序列进行下一步排序,不需要将另一端序列进行排序。实现代码如下:
1 class Solution {
2 public:
3 // 分区函数,每次返回一个下标值,该下标值表示已排好的数
4 int partition(vector<int>& nums, int low, int high) {
5 int temp = nums[low];
6 //对数列进行遍历,将比temp小的数搬到左边,比temp大的数搬到右边。
7 while(low < high) {
8 while((low < high) && (nums[high] > temp))
9 high--;
10 if(low < high)
11 nums[low++] = nums[high];
12 while((low < high) && (nums[low] < temp))
13 low ++;
14 if(low < high)
15 nums[high--] = nums[low];
16 }
17 nums[low] = temp;
18 return low;
19 }
20 void quicksort(vector<int>& nums, int low, int high, int k) {
21 if(low < high) {
22 // 对所得的两段序列进行判断,第K大的数在哪个序列中,则对哪个序列进一步排序。
23 int mid = partition(nums,low,high);
24 if(mid > nums.size() - k)
25 quicksort(nums,low,mid-1,k);
26 if(mid < nums.size() - k)
27 quicksort(nums,mid+1,high,k);
28 }
29 }
30 int findKthLargest(vector<int>& nums, int k) {
31 quicksort(nums, 0, nums.size()-1,k);
32 return nums[nums.size() - k];
33 }
34 };
Kth Largest Element in an Array
标签:cto for strong 合并 image sort函数 选择排序 排序 一段
原文地址:http://www.cnblogs.com/MT-ComputerVision/p/6505234.html