标签:开始 时间 分享 情况 简单 logs 提取 最坏情况 i+1
在程序中,人们经常关心的是程序运行时间。比如我们较早接触到的起泡排序,对于长度为n的序列A[0,n-1],我们比较A[i]和A[i+1]的大小,当A[i]<=A[i+1]时我们称这两个元素是顺序的,否则我们称这两个元素是逆序的,当两个元素逆序时,我们交换两个元素的位置,我们依次扫描序列A,当到达序列尾部时结束,这我们称完成了一趟扫描,由于每次至少能确定一个较大元素的位置,所以在进行了n-1趟扫描后程序结束。
下图为一个随机的数组
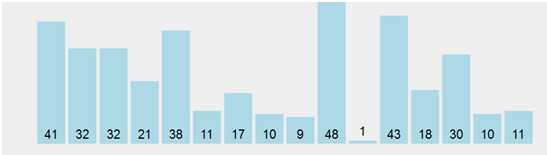
用冒泡排序扫描一趟后的结果为
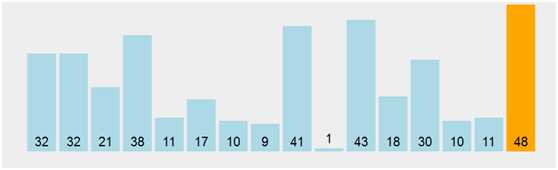
那么这个程序运行的时间是多少呢?显然其相关的因素很多。n的大小,序列本身的有序程度,不同的机器都有可能导致程序的执行时间不相同。这样的话问题就过于复杂,于是我们需要考虑一个理想的计算机,在这个计算机中每一个基本操作都是常数时间,这样我们就可以通过考察算法需要执行的次数来间接考察这个算法的执行时间。但是在序列有序和序列无序的情况下,元素交换的次数明显不同,从保守角度出发,我们选择最坏的结果作为T(n)。
现在,算法的时间复杂度T(n)=最坏情况下所须执行基本操作的次数,其中n是问题的规模。在现实中,我们更愿意关注问题规模不断变大时的算法复杂度,因为规模小时通常我们处理问题的开销也比较小。为此,我们引入了大O记号。
若存在正的常数c和函数f(n),使得当n>>2时,有T(n)<=c·f(n),则可认为f(n)是T(n)的渐进上界,记为T(n)=O(f(n))。
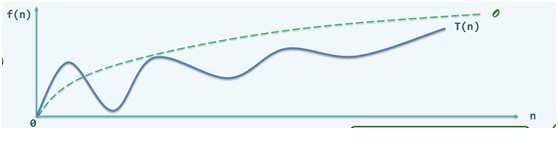
从图像上看出,f(n)是存在的,大O记号的存在使我们用一个更简单的函数来描述T(n)的上界。在有更好的办法分析算法的时间复杂度之前,进行了一个定量与定性之间的折中。
大O记号有两个重要的性质:
1) 对任意常数c>0,有O(f(n))=O(c·f(n))
2) 对任意常数a>b>0,有O(n^a+n^b)=O(n^a)
由于性质1,我们可以在时间复杂度的上界函数中提取任意常数。
由于性质2,我们可以忽略多项式中最高次幂以外的项。
现在,我们继续讨论文章开始的起泡排序,我们把元素的比较和交换作为基本操作,最糟糕情况下,每一轮进行n-1次比较,并进行n-1次交换,在执行了n-1轮后排序完成,则有T(n)=2(n-1)^2=n^2-4n+2。T(n)=O(4n^2-4n+2)=O(n^2)。由此我们得到了一个简单的复杂度度量方式。
标签:开始 时间 分享 情况 简单 logs 提取 最坏情况 i+1
原文地址:http://www.cnblogs.com/patchouli/p/6507530.html