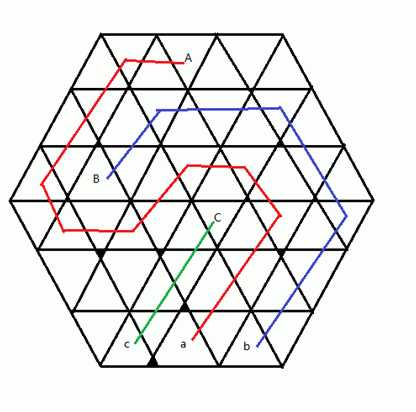
在2xyz年,人类已经移民到了火星上。由于工业的需要,人们开始在火星上采矿。火星的矿区是一个边长为N的正六边形,为了方便规划,整个矿区被分为6*N*N个正三角形的区域(如图1)。
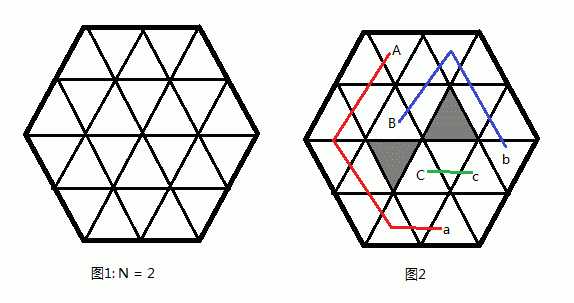
整个矿区中存在A矿,B矿,C矿三个矿场,和a厂,b厂,c厂三个炼矿厂。每个三角形的区域可以是一个矿场、炼矿厂、山地、或者平地。现在矿区管理局要求建立一个交通系统,使得矿场和对应炼矿厂之间存在一条公路,并且三条公路互不交叉(即一个三角形区域中不存在两条以上运输不同矿的公路)。两个三角形区域是相邻的当且仅当这两个三角形存在公共边,只有相邻的两个区域之间才能建一段路,建这段路的费用为1。注意,山地上是不能建公路的。由于火星金融危机的影响,矿区管理局想知道建立这样一个交通系统最少要花多少费用。更多的,当局向知道有多少种花费最小的方案。
第1行一个整数N。表示这个矿区是边长为N的正六边形。
接下来有6*N*N的整数,分为2*N行,表示矿区当前区域的情况。0表示平地,1,2,3表示对应的矿区或者炼矿厂,4表示山地。(样例1对应图2)。可能有多组数据,请处理到文件结尾
对于每组数据,包含两个整数,表示最小费用和达到最小费用的方案数。如果找不到符合要求的方案,输出-1 -1。由于方案数可能过大,所以请把方案数mod 1000000007
//40分dfs
//插头dp不会
#include<cstdio>
#include<cstring>
using namespace std;
const int N=70;
const int dx[2][3]={{1,0,0},{-1,0,0}};
const int dy[2][3]={{0,1,-1},{0,1,-1}};
int n,sx[4],sy[4],ex[4],ey[4],mp[N][N];bool vis[N][N];
int ans,sum;
inline void Cl(){
memset(mp,-1,sizeof mp);
memset(vis,0,sizeof vis);
memset(sx,0,sizeof sx);
memset(sy,0,sizeof sy);
memset(ex,0,sizeof ex);
memset(ey,0,sizeof ey);
}
inline void init(){
for(int i=1;i<=n;i++){
for(int j=n-i+1;j<=n*3+i-1;j++){
scanf("%d",&mp[i][j]);
int &db=mp[i][j];
if(db>0&&db<4){
if(!sx[db]) sx[db]=i,sy[db]=j;
else ex[db]=i,ey[db]=j;
}
}
}
for(int i=1;i<=n;i++){
for(int j=i;j<=n*4-i;j++){
scanf("%d",&mp[i+n][j]);
int &db=mp[i+n][j];
if(db>0&&db<4){
if(!sx[db]) sx[db]=i+n,sy[db]=j;
else ex[db]=i+n,ey[db]=j;
}
}
}
}
void dfs(int now,int x,int y,int cost){
if(x==ex[now]&&y==ey[now]){
if(now<3){
vis[sx[now+1]][sy[now+1]]=1;
dfs(now+1,sx[now+1],sy[now+1],cost);
vis[sx[now+1]][sy[now+1]]=0;
}
else{
if(cost==ans) sum++;
if(cost<ans) ans=cost,sum=1;
}
return ;
}
int p=!((x+y&1)^(n&1));
for(int i=0,nx,ny;i<3;i++){
nx=x+dx[p][i];ny=y+dy[p][i];
if(!vis[nx][ny]&&(!mp[nx][ny]||mp[nx][ny]==now)){
vis[nx][ny]=1;
dfs(now,nx,ny,cost+1);
vis[nx][ny]=0;
}
}
}
inline void work(){
Cl();init();
ans=2e9;sum=0;
vis[sx[1]][sy[1]]=1;
dfs(1,sx[1],sy[1],0);
if(sum) printf("%d %d\n",ans,sum);
else printf("-1 -1\n");
}
int main(){
freopen("mars.in","r",stdin);
freopen("mars.ans","w",stdout);
while(~scanf("%d",&n)) work();
return 0;
}