标签:技术分享 log 思想 机器学习 style 9.png 价格 房价 线性
线性回归的主要思想是:
已知样本数目为m,特征(feature)数目为n。
给出假设h(X)=theta0+theta1*x1+theta2*x2+…+thetan*xn=X*theta
X=[1,x1,x2,…xn],xi即第i个特征的值(这里默认利用向量同时处理m个样本值,即xi为m*1的向量),theta=[theta0,theta1,…,thetan]。
成本函数为J=sum((h(X)-Y)^2)/m,Y为实际值。
为最小化成本函数,使用梯度下降算法不断更新theta,然后基于假设找到最优值(可能是局部最优)。
以房子价格与房子特征(如房子面积、卧室数目等)之间的关系为例:
1.特征归一化
对某一个特征进行处理:xi=(x-mean(xi))/std(xi)
对多个特征同时处理:X=(X-mean(X))/std(X)
注:在MATLAB求均值和标准差,是按列处理。比如X大小为m*n,则mean(X)为1*n。
2.梯度下降更新theta
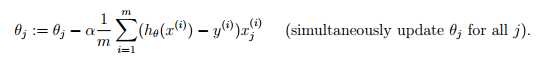
3.计算成本函数(作为检验)
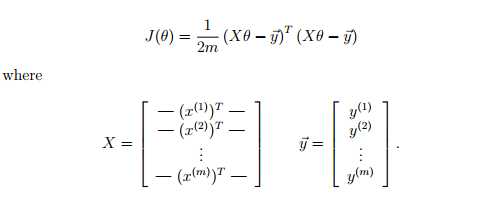
4.估计房价
给出特征值,比如现在有一间房有100平方米,2个卧室,则X=[1,100,2],基于最后更新得到的theta值,可以求出估计值。
最小二乘解(LS)
对成本函数取对数,然后求导使其导数为0,可得到最大似然估计的最小二乘解为:
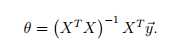
这样可以避免使用梯度下降进行多次迭代。
标签:技术分享 log 思想 机器学习 style 9.png 价格 房价 线性
原文地址:http://www.cnblogs.com/fanmu/p/6531724.html