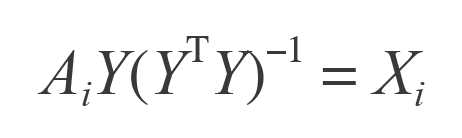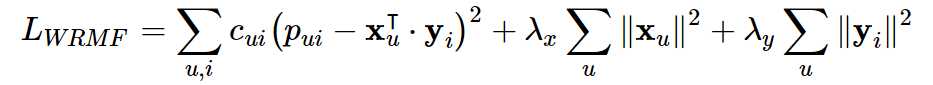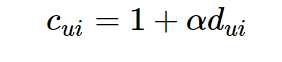R‘ = UTSV
然后再选取U中的K列和V中的S行作为隐特征的个数,达到降维的目的。K的选取通常用启发式策略。
这种方法有两个缺点,第一是补全成稠密矩阵之后需要耗费巨大的存储空间,在实际中,用户对物品的行为信息何止千万,对这样的稠密矩阵的存储是不现实的;第二,SVD的计算复杂度很高,更不用说这样的大规模稠密矩阵了。所以关于SVD的研究很多都是在小数据集上进行的。
隐语义模型也是基于矩阵分解的,但是和SVD不同,它是把原始矩阵分解成两个矩阵相乘而不是三个。
A = XYT
现在的问题就变成了确定X和Y ,我们把X叫做用户因子矩阵,Y叫做物品因子矩阵。通常上式不能达到精确相等的程度,我们要做的就是要最小化他们之间的差距,从而又变成了一个最优化问题。求解最优化问题我们很容易就想到了随机梯度下降,其中有一种方法就是这样,通过优化如下损失函数来找到X和Y中合适的参数:
其中puk就是X矩阵中u行k列的参数,度量了用户u和第k个隐类的关系;qik是Y矩阵中i行k列的参数,度量了物品i和第k个隐类的关系。这种方式也是一种很流行的方法,有很多对它的相关扩展,比如加上偏置项的LFM。
然而ALS用的是另一种求解方法,它先用随机初始化的方式固定一个矩阵,例如Y
然后通过最小化等式两边差的平方来更新另一个矩阵X,这就是“最小二乘”的由来。得到X之后,又可以固定X用相同的方法求Y,如此交替进行,直到最后收敛或者达到用户指定的迭代次数为止,是为“交替”是也。 从上式可以看出,X的第i行是A的第i行和Y的函数,因此可以很容易地分开计算X的每一行,这就为并行就算提供了很大的便捷,也正是如此,Spark这种面向大规模计算的平台选择了这个算法。在3这篇文章中,作者用了embarrassingly parallel来形容这个算法,意思是高度易并行化的——它的每个子任务之间没有什么依赖关系。
在现实中,不可能每个用户都和所有的物品都有行为关系,事实上,有交互关系的用户-物品对只占很小的一部分,换句话说,用户-物品关系列表是非常稀疏的。和SVD这种矩阵分解不同,ALS所用的矩阵分解技术在分解之前不用把系数矩阵填充成稠密矩阵之后再分解,这不但大大减少了存储空间,而且spark可以利用这种稀疏性用简单的线性代数计算求解。这几点使得本算法在大规模数据上计算非常快,解释了为什么spark mllib目前只有ALS一种推荐算法。
显性反馈和隐性反馈
我们知道,在推荐系统中用户和物品的交互数据分为显性反馈和隐性反馈数据的。在ALS中这两种情况也是被考虑了进来的,分别可以训练如下两种模型:val model1 = ALS.train(ratings, rank, numIterations, lambda)//显性反馈模型val model2 = ALS.trainImplicit(ratings, rank, numIterations, lambda, alpha)//隐性反馈模型
参数:
rating:由用户-物品矩阵构成的训练集
rank:隐藏因子的个数
numIterations: 迭代次数
lambda:正则项的惩罚系数
alpha: 置信参数
从上面可以看到,隐式模型多了一个置信参数,这就涉及到ALS中对于隐式反馈模型的处理方式了——有的文章称为“加权的正则化矩阵分解”,它的损失函数如下:
我们知道,在隐反馈模型中是没有评分的,所以在式子中rui被pui所取代,pui是偏好的表示,仅仅表示用户和物品之间有没有交互,而不表示评分高低或者喜好程度。比如用户和物品之间有交互就让pui等于1,没有就等于0。函数中还有一个cui的项,它用来表示用户偏爱某个商品的置信程度,比如交互次数多的权重就会增加。如果我们用dui来表示交互次数的话,那么就可以把置信程度表示成如下公式:
这里的alpha就是上面提到的置信参数,也是这个模型的超参数之一,需要用交叉验证来得到。
用spark的ALS模型进行推荐
1.为指定用户进行topN推荐
model.recommendProducts(userID, N)
2.为 用户-物品 对进行预测评分,显式和隐式反馈都可以,是根据两个因子矩阵对应行列相乘得到的数值,可以用来评估系统。既可以传入一对参数,也可以传入以(user,item)对类型的RDD对象作为参数,如下
model.predict(user, item)model.predict(RDD[int, int])
3.根据物品推荐相似的物品