某海量用户网站,用户拥有积分,积分可能会在使用过程中随时更新。现在要为该网站设计一种算法,在每次用户登录时显示其当前积分排名。用户最大规模为2亿;积分为非负整数,且小于100万。
首先,我们用一张用户积分表user_score来保存用户的积分信息。
表结构:
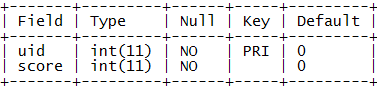
示例数据:
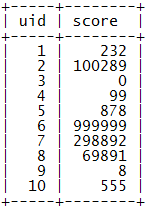
下面的算法会基于这个基本的表结构来进行。
首先,我们很容易想到用一条简单的SQL语句查询出积分大于该用户积分的用户数量:
select 1 + count(t2.uid) as rank
from user_score t1, user_score t2
where t1.uid = @uid and t2.score > t1.score
对于4号用户我们可以得到下面的结果:

算法特点
优点:简单,利用了SQL的功能,不需要复杂的查询逻辑,也不引入额外的存储结构,对小规模或性能要求不高的应用不失为一种良好的解决方案。
缺点:需要对user_score表进行全表扫描,还需要考虑到查询的同时若有积分更新会对表造成锁定,在海量数据规模和高并发的应用中,性能是无法接受的。
在许多应用中缓存是解决性能问题的重要途径,我们自然会想能不能把用户排名用Memcached缓存下来呢?不过再一想发现缓存似乎帮不上什么忙,因为用户排名是一个全局性的统计性指标,而并非用户的私有属性,其他用户的积分变化可能会马上影响到本用户的排名。然而,真实的应用中积分的变化其实也是有一定规律的,通常一个用户的积分不会突然暴增暴减,一般用户总是要在低分区混迹很长一段时间才会慢慢升入高分区,也就是说用户积分的分布总体说来是有区段的,我们进一步注意到高分区用户积分的细微变化其实对低分段用户的排名影响不大。于是,我们可以想到按积分区段进行统计的方法,引入一张分区积分表score_range:
表结构:

数据示例:
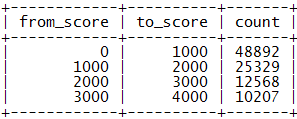
表示[from_score, to_score)区间有count个用户。若我们按每1000分划分一个区间则有[0, 1000), [1000, 2000), …, [999000, 1000000)这1000个区间,以后对用户积分的更新要相应地更新score_range表的区间值。在分区积分表的辅助下查询积分为s的用户的排名,可以首先确定其所属区间,把高于s的积分区间的count值累加,然后再查询出该用户在本区间内的排名,二者相加即可获得用户的排名。
乍一看,这个方法貌似通过区间聚合减少了查询计算量,实则不然。最大的问题在于如何查询用户在本区间内的排名呢?如果是在算法1中的SQL中加上积分条件:
select 1 + count(t2.uid) as rank
from user_score t1, user_score t2
where t1.uid = @uid and t2.score > t1.score and t2.score < @to_score
在理想情况下,由于把t2.score的范围限制在了1000以内,如果对score字段建立索引,我们期望本条SQL语句将通过索引大大减少扫描的user_score表的行数。不过真实情况并非如此,t2.score的范围在1000以内并不意味着该区间内的用户数也是1000,因为这里有积分相同的情况存在!二八定律告诉我们,前20%的低分区往往集中了80%的用户,这就是说对于大量低分区用户进行区间内排名查询的性能远不及对少数的高分区用户,所以在一般情况下这种分区方法不会带来实质性的性能提升。
算法特点
优点:注意到了积分区间的存在,并通过预先聚合消除查询的全表扫描。
缺点:积分非均匀分布的特点使得性能提升并不理想。
均匀分区查询算法的失败是由于积分分布的非均匀性,那么我们自然就会想,能不能按二八定律,把score_range表设计为非均匀区间呢?比如,把低分区划密集一点,10分一个区间,然后逐渐变成100分,1000分,10000分 … 当然,这不失为一种方法,不过这种分法有一定的随意性,不容易把握好,而且整个系统的积分分布会随着使用而逐渐发生变化,最初的较好的分区方法可能会变得不适应未来的情况了。我们希望找到一种分区方法,既可以适应积分非均匀性,又可以适应系统积分分布的变化,这就是树形分区。
我们可以把[0, 1,000,000)作为一级区间;再把一级区间分为两个2级区间[0, 500,000), [500,000, 1,000,000),然后把二级区间二分为4个3级区间[0, 250,000), [250,000, 500,000), [500,000, 750,000), [750,000, 1,000,000),依此类推,最终我们会得到1,000,000个21级区间[0,1), [1,2) … [999,999, 1,000,000)。这实际上是把区间组织成了一种平衡二叉树结构,根结点代表一级区间,每个非叶子结点有两个子结点,左子结点代表低分区间,右子结点代表高分区间。树形分区结构需要在更新时保持一种不变量(Invariant):非叶子结点的count值总是等于其左右子结点的count值之和。
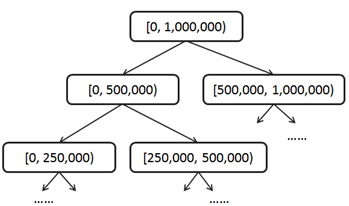
以后,每次用户积分有变化所需要更新的区间数量和积分变化量有关系,积分变化越小更新的区间层次越低。总体上,每次所需要更新的区间数量是用户积分变量的log(n)级别的,也就是说如果用户积分一次变化在百万级,更新区间的数量在二十这个级别。在这种树形分区积分表的辅助下查询积分为s的用户排名,实际上是一个在区间树上由上至下、由粗到细一步步明确s所在位置的过程。比如,对于积分499,000,我们用一个初值为0的排名变量来做累加;首先,它属于1级区间的左子树[0, 500,000),那么该用户排名应该在右子树[500,000, 1,000,000)的用户数count之后,我们把该count值累加到该用户排名变量,进入下一级区间;其次,它属于3级区间的[250,000, 500,000),这是2级区间的右子树,所以不用累加count到排名变量,直接进入下一级区间;再次,它属于4级区间的…;直到最后我们把用户积分精确定位在21级区间[499,000, 499,001),整个累加过程完成,得出排名!
虽然,本算法的更新和查询都涉及到若干个操作,但如果我们为区间的from_score和to_score建立索引,这些操作都是基于键的查询和更新,不会产生表扫描,因此效率更高。另外,本算法并不依赖于关系数据模型和SQL运算,可以轻易地改造为NoSQL等其他存储方式,而基于键的操作也很容易引入缓存机制进一步优化性能。进一步,我们可以估算一下树形区间的数目大约为2,000,000,考虑每个结点的大小,整个结构只占用几十M空间。所以,我们完全可以在内存建立区间树结构,并通过user_score表在O(n)的时间内初始化区间树,然后排名的查询和更新操作都可以在内存进行。一般来讲,同样的算法,从数据库到内存算法的性能提升常常可以达到10^5以上;因此,本算法可以达到非常高的性能。
算法特点
优点:结构稳定,不受积分分布影响;每次查询或更新的复杂度为积分最大值的O(log(n))级别,且与用户规模无关,可以应对海量规模;不依赖于SQL,容易改造为NoSQL或内存数据结构。
缺点:算法相对更复杂。
代码如下:
#include<iostream>
using namespace std;
struct BinaryTree
{
int count;// 该节点的孩子总数
int from_score;
int to_score;
BinaryTree* left;
BinaryTree* right;
BinaryTree(int from,int to,int c = 0):from_score(from),to_score(to),count(c),left(NULL),right(NULL){}
};
BinaryTree* createTree(BinaryTree*& root,int from,int to)
{
if(from > to)return NULL;
root = new BinaryTree(from,to);
if(from == to)return root;
int mid = from + ((to - from) >> 1);
root -> left = createTree(root -> left,from,mid);
root -> right = createTree(root->right,mid+1,to);
return root;
}
void insertNewScore(BinaryTree* root,int score)
{
if(root == NULL)return;
if(score >= root->from_score && score <= root->to_score)(root -> count) ++;
int mid = root->from_score + ((root->to_score-root->from_score) >> 1);
if(score <= mid)insertNewScore(root -> left,score);
else insertNewScore(root->right,score);
}
void deleteOldScore(BinaryTree* root,int score)
{
if(root == NULL)return;
if(score >= root->from_score && score <= root->to_score)(root -> count) --;
int mid = root->from_score + ((root->to_score-root->from_score) >> 1);
if(score <= mid)deleteOldScore(root -> left,score);
else deleteOldScore(root->right,score);
}
/* 更改score */
void changeScore(BinaryTree* root,int oldScore,int newScore)
{
deleteOldScore(root,oldScore);
insertNewScore(root,newScore);
}
void getRank(BinaryTree* root,int score,int& rank)
{
if(root == NULL)return;
int mid = root->from_score + ((root->to_score-root->from_score) >> 1);
if(score > mid)getRank(root->right,score,rank);
else if(root -> right)
{
rank += root -> right -> count;
getRank(root->left,score,rank);
}
}
int getRank(BinaryTree* root,int score)
{
int rank = 1;
getRank(root,score,rank);
return rank;
}
void print(BinaryTree* root)
{
if(root)
{
print(root -> left);
cout << root -> from_score << " " << root -> to_score << " " << root -> count << endl;
print(root -> right);
}
}
int main()
{
BinaryTree* root = NULL;
createTree(root,1,10);//建立排名树
int score[10] = {1,3,5,6,2,4,3,1,7,7};
for(int i = 0;i < 10;i++)insertNewScore(root,score[i]);
cout << "------------初始化后----------------" << endl;
print(root);
cout << "------------5的排名-----------------" << endl;
cout << getRank(root,5) << endl;
cout << "------------改变score----------------" << endl;
changeScore(root,2,4);
print(root);
cout << "-------------3的排名----------------" << endl;
cout << getRank(root,3) << endl;
}算法3虽然性能较高,达到了积分变化的O(log(n))的复杂度,但是实现上比较复杂。另外,O(log(n))的复杂度只在n特别大的时候才显出它的优势,而实际应用中积分的变化情况往往不会太大,这时和O(n)的算法相比往往没有明显的优势,甚至可能更慢。
考虑到这一情况,仔细观察一下积分变化对排名的具体影响,可以发现某用户的积分从s变为s+n,积分小于s或者大于等于s+n的其他用户排名实际上并不会受到影响,只有积分在[s,s+n)区间内的用户排名会下降1位。我们可以用于一个大小为1,000,000的数组表示积分和排名的对应关系,其中rank[s]表示积分s所对应的排名。初始化时,rank数组可以由user_score表在O(n)的复杂度内计算而来。用户排名的查询和更新基于这个数组来进行。查询积分s所对应的排名直接返回rank[s]即可,复杂度为O(1);当用户积分从s变为s+n,只需要把rank[s]到rank[s+n-1]这n个元素的值增加1即可,复杂度为O(n)。
算法特点
优点:积分排名数组比区间树更简单,易于实现;排名查询复杂度为O(1);排名更新复杂度O(n),在积分变化不大的情况下非常高效。
缺点:当n比较大时,需要更新大量元素,效率不如算法3。
上面介绍了用户积分排名的几种算法,算法1简单易于理解和实现,适用于小规模和低并发应用;算法3引入了更复杂的树形分区结构,但是O(log(n))的复杂度性能优越,可以应用于海量规模和高并发;算法4采用简单的排名数组,易于实现,在积分变化不大的情况下性能不亚于算法3。本问题是一个开放性的问题,相信一定还有其他优秀的算法和解决方案,欢迎探讨!
4. 在实际应用中,还有一个“精确度”的问题。我们可能并不需要返回严格意义上的最大的K个元素,在边界位置允许出现一些误差。当用户输入一个query的时候,对于每一个文档d来说,它跟这个query之间都有一个相关性衡量权重f (query, d)。搜索引擎需要返回给用户的就是相关性权重最大的K个网页。如果每页10个网页,用户不会关心第1000页开外搜索结果的“精确度”,稍有误差是可以接受的。比如我们可以返回相关性第10 001大的网页,而不是第9999大的。在这种情况下,算法该如何改进才能更快更有效率呢?网页的数目可能大到一台机器无法容纳得下,这时怎么办呢?
提示:归并排序?如果每台机器都返回最相关的K个文档,那么所有机器上最相关K个文档的并集肯定包含全集中最相关的K个文档。由于边界情况并不需要非常精确,如果每台机器返回最好的K’个文档,那么K’应该如何取值,以达到我们返回最相关的90%*K个文档是完全精确的,或者最终返回的最相关的K个文档精确度超过90%(最相关的K个文档中90%以上在全集中相关性的确排在前K),或者最终返回的最相关的K个文档最差的相关性排序没有超出110%*K。
网上答案:答:正如提示中所说,可以让每台机器返回最相关的K‘个文档,然后利用归并排序的思想,得到所有文档中最相关的K个。 最好的情况是这K个文档在所有机器中平均分布,这时每台机器只要K‘ = K / n (n为所有机器总数);最坏情况,所有最相关的K个文档只出现在其中的某一台机器上,这时K‘需近似等于K了。我觉得比较好的做法可以在每台机器上维护一个堆,然后对堆顶元素实行归并排序。5. 如第4点所说,对于每个文档d,相对于不同的关键字q1, q2, …, qm,分别有相关性权重f(d, q1),f(d, q2), …, f(d, qm)。如果用户输入关键字qi之后,我们已经获得了最相关的K个文档,而已知关键字qj跟关键字qi相似,文档跟这两个关键字的权重大小比较靠近,那么关键字qi的最相关的K个文档,对寻找qj最相关的K个文档有没有帮助呢?
解答:肯定是有帮助的。 qi最相关的K个文档可能就是qj的最相关的K个文档,可以先假设这K个就是,然后根据问题四的解法获得K‘,分别和这K个比较,可以用堆进行比较,从而获得qj最相关的K个文档。由于最开始的K个文档极有可能是最终的K个文档,所以K‘和K比较的次数可能并不多。
原文地址:http://blog.csdn.net/fangjian1204/article/details/38733997