标签:gre 1.0 break abs 展开 margin ati .cpp black
SVM -支持向量机原理详解与实践之四
SMO即Sequential minmal optimization, 是最快的二次规划的优化算法,特使对线性SVM和稀疏数据性能更优。在正式介绍SMO算法之前,首先要了解坐标上升法。
坐标上升法(Coordinate Ascent)简单点说就是它每次通过更新函数中的一维,通过多次的迭代以达到优化函数的目的。
为了更加通用的表示算法的求解过程,我们将算法表示成:
|
|
(3.13-1) |
坐标上升法的算法为:
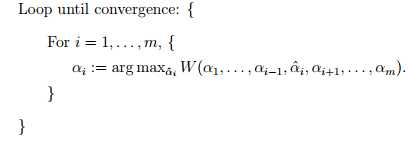
这个算法中最为关键的地方就是内循环对于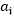 的求解,意思是固定除了
的求解,意思是固定除了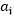 之外的所有a(从i=1~m),也就是说将
之外的所有a(从i=1~m),也就是说将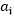 除外的其他变量看成是常数,并且将W看做是关于
除外的其他变量看成是常数,并且将W看做是关于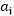 的函数,那么直接对
的函数,那么直接对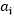 求导优化得到极大值,在上面算法的版本中,内循环优化变量的顺序是
求导优化得到极大值,在上面算法的版本中,内循环优化变量的顺序是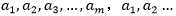 但是一个更高级的版本可能选择其它的顺序,例如我可以根据我们的期望来选择下一个变量来更新,并让W(a)有最大的增加。
但是一个更高级的版本可能选择其它的顺序,例如我可以根据我们的期望来选择下一个变量来更新,并让W(a)有最大的增加。
当函数W在内循环中能够最快的达到最优,则坐标上升是一个有效的算法,下面是一个坐标上升的示意图:
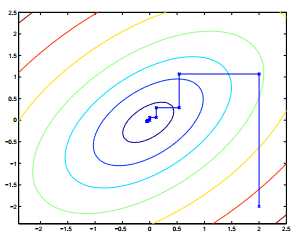
上图中的椭圆形线代表我们需要优化问题的二次函数的等高线,变量数为2,起始坐标是(2,2),途中的直线是迭代优化的路径,可以看到每一步都会相最优值前进一步,而且前进的路线都是平行与相应的坐标轴的,因为每次只优化一个变量。
问题:求解函数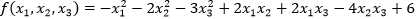 的最大值。
的最大值。
解:回顾我们前面分析的求取函数最大值的关键是,求解每一个迭代变量的导数,当求解某一变量的导数的时候,其他的变量看做是常数:
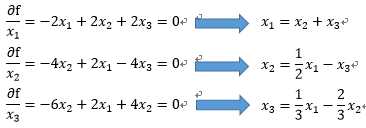
VS2013控制台工程参考代码如下:
// Coordinate ascent.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include <iostream>
using namespace std;
#define f(x1,x2,x3) (-x1*x1-2*x2*x2-3*x3*x3+2*x1*x2+2*x1*x3-4*x2*x3+6)
int _tmain(int argc, _TCHAR* argv[])
{
double x1 = 1;
double x2 = 1;
double x3 = 1;
double f0 = f(x1, x2, x3);
double err = 1.0e-10;
while (true)
{
x1 = x2 + x3; //对x1求导的表达式,每次迭代后更新
x2 = 0.5*x1 - x3; //对x2求导的表达式,每次迭代后更新
x3 = 1.0 / 3 * x1 - 2.0 / 3 * x2; //对x3求导的表达式,每次迭代后更新
double ft = f(x1, x2, x3); //求函数值
if (abs(ft - f0)<err) //判断f是否收敛
{
break; //收敛即完成求解过程
}
f0 = ft; //更新f0
}
cout << "\nmax{f(x1,x2,x3)}=" << f(x1, x2, x3) << endl;
cout << "取得最大值时的坐标:\n(x1,x2,x3)=(" << x1 << "," << x2 << "," << x3 << ")" << endl;
system("pause");
return 0;
}
运行结果如下:

回到我们软间隔与正则化章节(还有最优间隔分类器),我们的对偶问题,就是通过固定拉格朗日乘子a,得到w和b的最优化表达式(关于a的表达式),所以最后我们只需要确认a,我们就可以最终确定w和b,但是在讨论SMO算法之前,我们并没有真正求解出 。这一章我们就会通过介绍SMO算法对对偶问题最后需要解决的问题:
。这一章我们就会通过介绍SMO算法对对偶问题最后需要解决的问题:
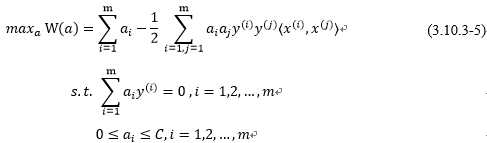
做出一个求解,也就是在参数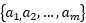 上求W最大值的问题,注意其中的
上求W最大值的问题,注意其中的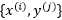 就是训练样本的输入,x即为样本的输入特征,y即样本对应的标签(结果)。
就是训练样本的输入,x即为样本的输入特征,y即样本对应的标签(结果)。
按照前面介绍的坐标上升的思路,我们首先固定除了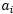 以外的所有参数,然后在
以外的所有参数,然后在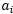 上求极值。现在下面先固定
上求极值。现在下面先固定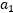 以外的所有参数,看看具体的求解步骤:
以外的所有参数,看看具体的求解步骤:
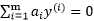 可知:
可知: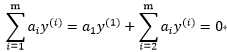
即可推出
|
|
|||
|
两边乘以: |
|
||
|
|
(3.13.2-1) |
||
因为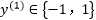 ,所以
,所以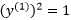 ,因此到这一步,
,因此到这一步,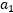 就由其它的
就由其它的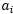 决定,如果我们固定主
决定,如果我们固定主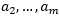 ,无论如何不能违背优化问题的约束
,无论如何不能违背优化问题的约束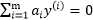 。
。
因此如果我们想要更新一些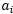 的对象,为了保持满足约束条件就必须至少快速的更新它们中的两个,这个就激发出SMO算法,那么SMO算法可以简单的描述成:
的对象,为了保持满足约束条件就必须至少快速的更新它们中的两个,这个就激发出SMO算法,那么SMO算法可以简单的描述成:
重复大括号中的操作直到收敛{
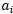 和
和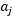 来更新下一个(用启发式的方法,也就是尝试选取两个允许我们朝着全局最大方向做最大前进的参数)。
来更新下一个(用启发式的方法,也就是尝试选取两个允许我们朝着全局最大方向做最大前进的参数)。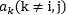 ,优化关于
,优化关于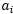 和
和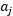 的函数W(a)。
的函数W(a)。}
为了测试该算法的收敛性,我们可以检查KKT条件:

是否满足收敛容错参数,典型值为0.1~0.001之间。
SMO作为一个高效的算法的关键原因在于计算更新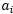 和
和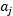 的效率非常高。假设当前我们有一些
的效率非常高。假设当前我们有一些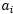 满足(3.10.3-5)的约束,固定
满足(3.10.3-5)的约束,固定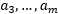 ,想要优化关于
,想要优化关于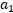 和
和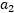 的函数,用
的函数,用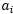 表示
表示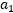 和
和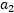 有:
有:
|
|
由于右边固定,我们可以直接用一个常数表示,例如用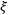 表示:
表示:
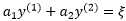
于是我可以将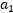 和
和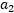 的约束画出来:
的约束画出来:
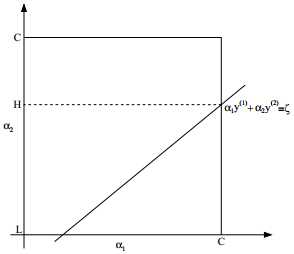
根据约束条件:
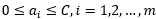
可知上图中表示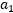 和
和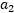 的横轴和纵轴必须限制在0到C的方框内,并且也要在直线上。并且
的横轴和纵轴必须限制在0到C的方框内,并且也要在直线上。并且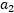 的纵轴也必须满足
的纵轴也必须满足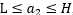 ,否则就不能满足约束条件。
,否则就不能满足约束条件。
下面用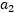 表示
表示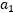 ,过程是:
,过程是:
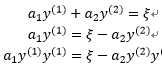
其中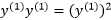 ,因为
,因为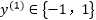 ,所以有:
,所以有:
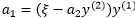
所以目标问题W可以表示为:
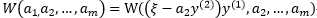
其中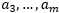 为常数。
为常数。
实际的问题中W展开后就是一个关于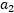 的二次函数
的二次函数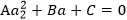 , A、B、C是固定值,这样通过对W进行求导可得
, A、B、C是固定值,这样通过对W进行求导可得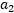 ,然而要保证
,然而要保证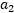 满足
满足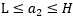 ,我们使用
,我们使用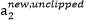 表示求导求出的
表示求导求出的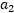 , 然而最后的
, 然而最后的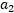 ,需要根据下面的情况得到:
,需要根据下面的情况得到:
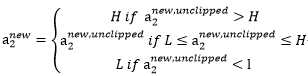
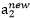 求出以后,我们可以就可以得到
求出以后,我们可以就可以得到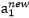 。
。
这里限于篇幅,实践的内容将在下一篇展开…
标签:gre 1.0 break abs 展开 margin ati .cpp black
原文地址:http://www.cnblogs.com/spoorer/p/6548885.html