标签：梯度 gbdt 0kb 方向 提升 生成 die gradient iss
提升是机器学习技术，可以用于回归和分类问题，它每一步产生一个弱预测模型（如决策树），并加权累加到总模型中；如果每一步的弱预测模型生成都市一句损失函数的梯度方向，则称之为梯度提升（Gradient boosting).
梯度提升算法首先给定一个目标函数，它的定义域是所有可行的弱函数集合（基函数）；提升算法通过迭代的选择一个负梯度方向上的基函数来逐渐逼近局部极小值。这种在函数域的梯度提升观点对机器学习的很多领域有深刻影响。
提升的理论意义：如果一个问题存在弱分类器，则可以通过提升的办法得到强分类器。
现在用公式来解释一下提升算法的大致思路。
给定输入向量x和输出向量y组成的若干训练样本： (x1,y1), (x2, y2),(x3, y3)…（xn, yn)。
目标是要找出一个近似函数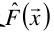
，使得损失函数L(y, F(x))的损失最小。
其中损失函数L(y, F(x))的形式有多种，比较典型为：
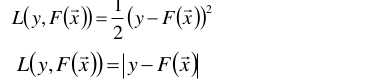
y是样本的实际值，F(x)是通过模型F预测出来的预测值，两者的差距就形成了损失。
也就是说，通过损失最小的目标函数，最终会求一个最优的函数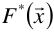
，那么这个最优的函数肯定是损失的期望最小的。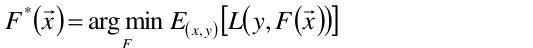 
现在已经很明确，目标是去求最优的F(X)函数，它做出的预测与实际的值的差距是最小的，也就是预测是最准的，这当然是我们求之不得的啦。那么怎么去求这个F(X)呢？
它是一个强预测模型，上面的概念里最后一句回答了，弱预测模型可以通过提升的方式变成强预测模型。
所以的所以，我们假定F(x)是一组基函数（弱预测函数）f(xi)的加权和。
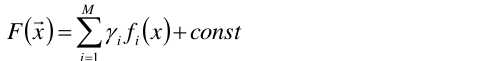
γ是每个基函数的权重。
于是问题变成了求取基函数，以及它们对应的权值γ。
要求得的最优函数F(X)是由一组基函数f(x)加权而来。
基函数：f0, f1, f2…fn
权值：γ0， γ1， γ2，…γn
首先，给定常函数F0(x)：
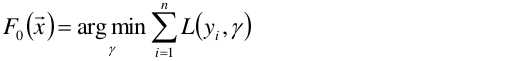
使得第一个基函数f0 = 1,所以F0(x)就简化为以上公式。以上函数中未知数为γ。目标是要求以上函数最小值时γ为多少，其实就是定义F0(x)求导=0， 求出来之后常系数γ=1/n。
于是现在我们有了f0和γ0，即第一个基函数与它的权值，即F0(x)。那么如何继续求接下去的基函数与权值呢？这里以贪心算法的思路扩展到Fm(x)（贪心算法就是运筹学里的动态规划）：
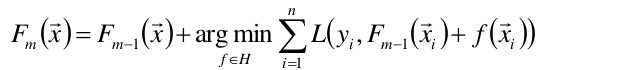
假设我们已经知道了Fm-1(x),即已经知道了f0,f1,…fm-1,与γ0，γ1…γm-1,可以将以上函数求出最优的f(xi),从而求得最优的Fm(x).
然而贪心法在每次选择最优基函数f时仍然困难。所以，选择使用梯度下降的方法来近似计算。过程是这样的：
将样本代入基函数f得到了f(x1), f(x2), …,f(xn),从而L退化维向量L(y1,f(x1)), L(y2, f(x2)),…,L(yn, f(xn))
于是可以对损失函数求f的偏导：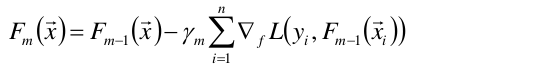 
上式的权值γ为梯度下降的步长，使用线性搜索求最优步长：
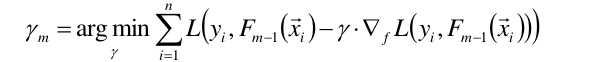
以前的梯度下降法是求出最小值时的那个x，现在是求最小值时的那个函数f（这个函数f有可能是决策树模型，逻辑回归模型等等）。
来来来，把上面的再理一下思路：
1.初始给定的模型为常数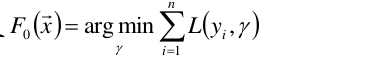
=1
2.对于m=1到M
（1）
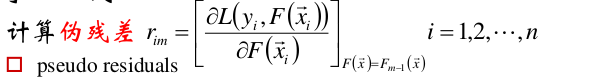
（2）使用数据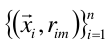
计算你和参差的基函数fm(x).
说人话，就是通过求得参差，我们有了一组新的数据
，假设这组数据是样本点，对这组样本点去求得一个分类器，这个分类器其实就是我们的基函数f。
（3）计算步长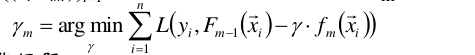
（4）更新模型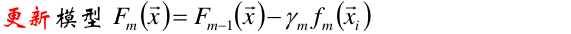
对重复以上的步骤一直到M，这就是GBDT梯度提升决策树。
标签：梯度 gbdt 0kb 方向 提升 生成 die gradient iss
原文地址：http://www.cnblogs.com/yuzhuwei/p/6551264.html
