标签:利用 暴力 计数 robot 欧拉回路 margin code 质因数 构造
最近做到了一些有趣的散题,于是开个Blog记录一下吧…
(如果有人想做这些题的话还是不要看题解吧…)
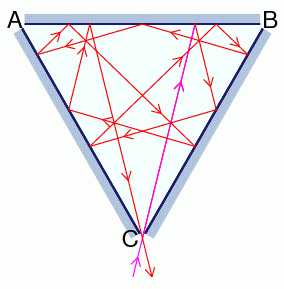
题意:有一个正三角形的镜子屋,光线从$C$点射入,求恰好反射$12017639147$次后在$C$点射出的方案数。
题解:关于反射问题容易想到对称性,不断对称翻转正三角形,可以密铺整个平面,这样一条反射$k$次的路径对应平面上经过$k$条边的路径。
然后取$CB,CA$为基,把平面画正,就能得到一个带有平行的对角线的网格图,稍微观察一下就能发现反射$2k+1$次就意味着目标点的$x+y=k$。
然后算上射出点必须在$C$点的限制,有$x \equiv y \pmod{3}$,并且为了不在之前从其他点射出,需要满足$(x+1,y+1)=1$。
于是变成一个计数题,因为$x+y$是固定的,所以求GCD时利用GCD的性质可以变成单独的$x+1$与常数互质的计数,暴力或者容斥都可以…
做的时候虽然不费什么力气就完成了第一步的转化,但是统计答案时我首先想的是暴力…感觉比较糟糕呀…为什么我老是那么暴力…
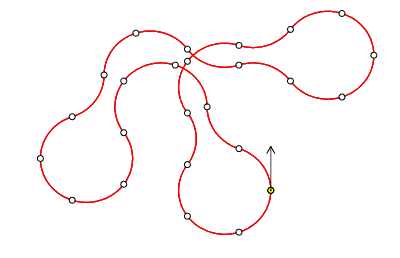
题意:有一个机器人,每步行动只能选择顺着当前方向顺时针或者逆时针转弯移动五分之一圆,求行动$70$步后恰好回到原点的方案数。
题解:一开始就有种很不好下手的感觉…因为直接考虑统计操作序列就难以表示回到原点的限制…而直接对着位置进行统计的话又会因为只能转弯的限制而变得不好统计…于是我开始考虑路径的嵌套,一开始的想法是先构造出绕若干圈的方案,然后再在中间插入延长路径的步骤…想想画画,很久之后突然发现是自己想多了…一开始就直接考虑各方向伸展的长度就好了,转弯的限制很容易就能转化为另一个问题…然后就轻易地变成每方向走$14$步,并且相邻两步的方向相差$1$的方案数。其实就是一个五个点的环且环上的边都是$14$重边的图的欧拉回路计数…没怎么想就直接暴力弄了个$5 \times 14^5$的DP算了…就这么暴力地解决了。
感觉这道题性质非常特殊呀…这种暴力地做法似乎浪费了那么好的性质,感觉不优美…不过我暂时没想到其它办法,以后多了解一点欧拉回路计数之后可能就会有更好的想法了。
题意:和题目名字一样,就是算一下$10^{16}$以内有多少数有至少$4$个$100$以内的质因数。
题解:一眼就能看出来是最简单的容斥原理…没什么好说的…不过我花了出奇长的时间…大概是对容斥的理解还不够深刻吧,最基本的$\pm 1$的容斥形式只是照着感觉和经验写的,而其中的道理却没有理解透,所以才会花那么久…明明容斥已经不知道用过多少次了,却还没弄清楚,真是得反思呀…其实只要知道当前状态被计数次数和它应该被计数次数的差就能得到容斥系数了,预先跑一次求出每种质因子个数的容斥系数就能算了。(最基本的容斥形式因为是从$1$开始的,所以得到的就会是$\pm 1$交替的系数,这里则是从$4$开始,所以会得到不一样的系数)
Codeforces/TopCoder/ProjectEuler 散题笔记 (持续更新)
标签:利用 暴力 计数 robot 欧拉回路 margin code 质因数 构造
原文地址:http://www.cnblogs.com/meowww/p/6561356.html