标签：推导 ict ges 理论 博客 特化 个人 笔记 res
？凸优化在数学优化中有着重要且特殊的身份。数学优化是一个广泛的话题，理解凸优化之前，请先理解线性优化。在机器学习算法中，已知的比如LogisticRegression,SVM,都与数学优化有关，在数学中，不存在无约束优化问题。比较常见的构建损失函数方法，从最简单的两个向量的二阶范数的平方(KNN,Kmeans)到linearRegression、LogisticRegression的最小二乘模型，再到SVM的二次凸优化，都和数学优化理论紧密相关。本篇笔记主要学习数学优化的前奏部分：凸优化的概念部分。
1.1.1数学优化
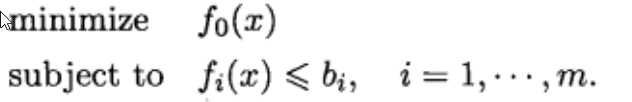--------------------①
这是数学优化的最基本形式。其中，x = (x1,x2,……xn)称为优化变量，函数
称为目标函数，函数
称为约束函数。常数
称为约束上限或者约束边界。如果在所有满足约束的向量中向量
对应的目标函数值最小，那么他就是问题的最优解。
在机器学习理论的推导中，一般只考虑特殊的优化问题，线性优化问题。对于上式，如果目标函数和约束函数都是线性函数，即对于任意的
和
，都有：
------------------------------------②
则此问题成为线性规划。在机器学习算法中，还需要进一步特化，就是凸优化。凸优化中目标函数和约束函数都属于凸函数，即对于任意的
，任意
，都有：
--------------------------------③成立。比较③和②式可以发现，③式是②式的特殊形式。只用在
或者
其中一个为0的情况下才成立。不同的是两者的严格程度，后者凸优化是不太严格的线性优化问题。所以可以用线性优化的手段来解决凸优化问题，甚至包括特殊情况下的非线性规划问题，也可以采取特殊手段往这个方向靠拢(目前在业内，对于非线性优化问题的求解还不算成熟)。上一篇博客中推导过LogisticRegression的似然函数（与损失函数取反），其实属于非严格意义上的凸优化问题,包括线性回归，这类问题的损失函数构建可以用最小二乘模型来解决，它本身属于线性优化问题的范畴。(对于凸函数的定义，有不同的说法。比如，一般认为二阶导数<0的函数属于凸函数，>0属于凹函数。因为二阶导数<0意味着一阶导数属于减函数，也就是原函数的切线的斜率是不断减小的，这种情况原函数就只能是先增后减了。)
对于凸优化问题，我们认为目标函数是成本函数，在优化变量满足约束的情况下，让成本或者损失最小。
1.1.2 线性优化问题的求解
在工程实际应用中，我们需要的是得到稀疏性的解，不仅可以减少迭代次数，还可以解决过拟合问题，增强模型的解释能力。关于sparse问题，有专门的研究课题(比如lasso学术研究，CD算法，LAR算法)，这里不讨论。对于优化问题的求解，有两类非常重要且广泛的求解方法：最小二乘法和线性规划问题。还有一类特殊的优化方法：凸优化。
1.2 最小二乘问题
在线性回归的损失函数的推导中，假定认为偏差(
= real - predict)遵循Gaussian Destribution（N(0,1)）,根据判别学习模型估计最大似然函数，最后得出来的结论其实是最小二乘模型。最小二乘问题是回归问题，最优控制以及很多参数估计和数据拟合方法的基础。在统计学中有着很重要的意义，比如给定包含高斯噪声的线性测量值时，似然函数的估计的最优解是最小二乘法。如果目标函数是二次函数并且半正定(开口朝上，并且函数值不全>0) ,他就是最小二乘问题。
用数学公式来解释，最小二乘问题属于特殊的数学优化问题，没有约束(m=0)。目标函数其实是由偏差组成的列向量的二阶范数的平方(个人理解),如下形式的优化：
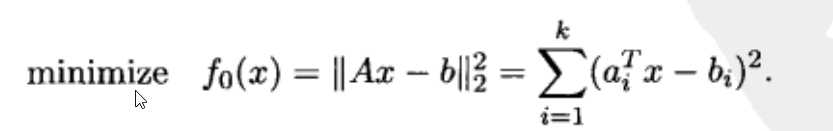--------------------------------------④
其中，A可以理解为机器学习中特征矩阵，x为估计参数，b为真实值组成的列向量，最后面的部分是拆解后的结果。在求解时，一般采用传统的在线学习方法SGD。
正则化是此类问题的热点。上个世纪90年代，有学者提出lasso，此后论文被引用了14000多次，由此可见lasso的重要性。在机器学习中，提高模型的泛化能力很重要。LogisticRegression的处理主要有岭回归和L1范数，关于这方面，专门写一篇博客。
1.2.2 线性规划
另一类比较重要的问题是线性规划。如下形式：
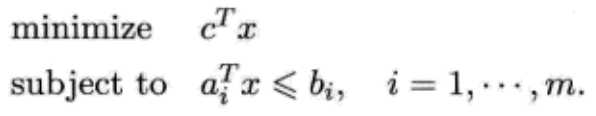-------------------⑤
。
标签：推导 ict ges 理论 博客 特化 个人 笔记 res
原文地址：http://www.cnblogs.com/txq157/p/6575553.html
