标签：ace ... 优化 auto 指针 复杂度 nes lin 运算
Given a n × n matrix A and a positive integer k, find the sum S = A + A2 + A3 + … + Ak.
Input
The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 109) and m (m < 104). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.
Output
Output the elements of S modulo m in the same way as A is given.
Sample Input
2 2 4 0 1 1 1
Sample Output
1 2 2 3
这道题直接暴力呢。。O(n3k)的时间复杂度，必死无疑。所以只能另寻出路，注意到矩阵满足分配律
“若A和B皆为n行p列的矩阵，C为p行m列的矩阵，则有
(A + B)C = AB + AC”
左分配律差不多（因为矩阵乘法不满足交换律，所有分配律又分为左分配律和右分配律）
证明就水水的写一下
对于A + B，我们有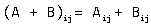
那么
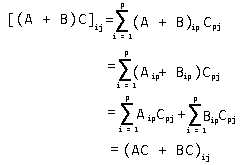
所以(A + B)C = AB + AC（我也不确定这样证明是正确的，但是思路可取）
因为有了分配律这个神奇东西，现在计算A + A2 + ... + A6的和，就等价于(A + A2 + A3) + A3(A + A2 + A3)
现在设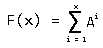
（x > 1）
那么一般地有
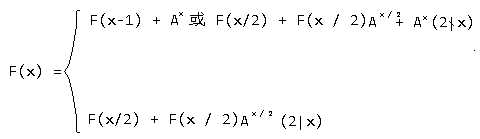
上面有一个或，意味着两种方式皆可，反正都很慢。
如果理论上应该是可以过的时间复杂度大概是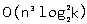
，但是如果代码写得比较丑就有TLE的风险，可以考虑一下以下优化
1）不要没事就作无用的初始化，很耗时间
2）降低取模次数
3）读入优化
4）不用重载运算符，指针和引用可以大量降低赋值的时间(反正我不存在这个问题，因为矩阵里用的指针，而不是数组)
1 /** 2 * poj 3 * Problem#3233 4 * Accepted 5 * Time:2266ms 6 * Memory:3892k 7 */ 8 #include<iostream> 9 #include<cstdio> 10 #include<cctype> 11 #include<cstring> 12 #include<cstdlib> 13 #include<fstream> 14 #include<sstream> 15 #include<algorithm> 16 #include<map> 17 #include<set> 18 #include<queue> 19 #include<vector> 20 #include<stack> 21 using namespace std; 22 typedef bool boolean; 23 #define INF 0xfffffff 24 #define smin(a, b) a = min(a, b) 25 #define smax(a, b) a = max(a, b) 26 template<typename T> 27 inline void readInteger(T& u){ 28 char x; 29 int aFlag = 1; 30 while(!isdigit((x = getchar())) && x != ‘-‘); 31 if(x == ‘-‘){ 32 x = getchar(); 33 aFlag = -1; 34 } 35 for(u = x - ‘0‘; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - ‘0‘); 36 ungetc(x, stdin); 37 u *= aFlag; 38 } 39 40 typedef class Matrix { 41 public: 42 int* p; 43 int lines, cols; 44 int moder; 45 Matrix():p(NULL), lines(0), cols(0), moder(1) { } 46 Matrix(int lines, int cols, int moder):lines(lines), cols(cols), moder(moder) { 47 p = new int[(lines * cols)]; 48 } 49 50 int* operator [](int pos) { 51 return p + pos * cols; 52 } 53 54 Matrix operator *(Matrix b) { 55 Matrix res(lines, b.cols, moder); 56 for(int i = 0; i < lines; i++) { 57 for(int j = 0; j < b.cols; j++) { 58 res[i][j] = 0; 59 for(int k = 0; k < cols; k++) { 60 (res[i][j] += (*this)[i][k] * b[k][j] % moder) %= moder; 61 } 62 } 63 } 64 return res; 65 } 66 67 Matrix operator +(Matrix b) { 68 Matrix res(lines, cols, moder); 69 for(int i = 0; i < lines; i++) 70 for(int j = 0; j < cols; j++) 71 res[i][j] = ((*this)[i][j] + b[i][j]) % moder; 72 return res; 73 } 74 }Matrix; 75 76 template<typename T> 77 T pow(T a, int pos) { 78 if(pos == 1) return a; 79 T temp = pow(a, pos / 2); 80 if(pos & 1) return temp * temp * a; 81 return temp * temp; 82 } 83 84 int n, k, m; 85 Matrix a; 86 87 inline void init() { 88 readInteger(n); 89 readInteger(k); 90 readInteger(m); 91 a = Matrix(n, n, m); 92 for(int i = 0; i < n; i++) { 93 for(int j = 0; j < n; j++) { 94 readInteger(a[i][j]); 95 a[i][j] %= m; 96 } 97 } 98 } 99 100 template<typename T> 101 T pow_sum(T a, int pos) { 102 if(pos == 1) return a; 103 T temp = pow_sum(a, pos / 2); 104 temp = temp + temp * pow(a, pos / 2); 105 if(pos & 1) return temp + pow(a, pos); 106 return temp; 107 } 108 109 Matrix res; 110 inline void solve() { 111 res = pow_sum(a, k); 112 for(int i = 0; i < n; i++) { 113 for(int j = 0; j < n; j++) { 114 printf("%d ", res[i][j]); 115 } 116 putchar(‘\n‘); 117 } 118 } 119 120 int main() { 121 init(); 122 solve(); 123 return 0; 124 }
poj 3233 Matrix Power Series - 矩阵快速幂
标签：ace ... 优化 auto 指针 复杂度 nes lin 运算
原文地址：http://www.cnblogs.com/yyf0309/p/6576035.html
