标签:read 不同 new vnode 保存 method stat bfs tac
1.解决问题:判断一幅图中 从顶点S到顶点V之间是否有一条路径---Dijkstar算法的基础(计算出S--V点中最短路径)
1.使用队列(FIFO)先进先出原则 存储与顶点S相距 N条边的点,直到遍历到V点上 不同于深度优先遍历 不需要进行递归 因此 BFS无法判断图中是否有环的
判断出一个有向图是否有环的是:a.最短路径有向图最短路径Dijkstra不一定能够判断有环,除非Visted数字记录0(false),1(已经访问)2(再一次重复访问);
b.括扑排序:通过入度0之后记录顶点数与原Vetex相比较;括扑排序只是处理入度为零的算法形式
c.DFS(深度优先遍历),图处理成树结构时候,找到一个节点保存节点,DFS找到重复节点表面图中有环
d.但是BFS(广度优先遍历),层次遍历方式,A->C,B->C,图中两条边指向一个公共点C,nodeC访问重复,但是不能判断其中出现环情况
1 package Graph; 2 3 import java.util.LinkedList; 4 import java.util.Queue; 5 import java.util.Stack; 6 7 public class BreadthFirstPath { 8 public Graph G; 9 public boolean [] marked; 10 private int[] edgeTo;// 记录根结点到其点顶点的路径 11 12 public BreadthFirstPath(Graph G ,int s) 13 { 14 this.G=G; 15 marked=new boolean[G.Vertex]; 16 edgeTo=new int[G.Vertex]; 17 bfs(G,s); 18 //System.out.println("输出结果"); 19 pathTo(4,0); 20 } 21 public void pathTo(int v,int st) 22 { 23 Stack<Integer> path=new Stack<Integer>(); 24 for(int x=v;x!=st;x=edgeTo[x]) 25 { 26 path.add(x); 27 } 28 path.add(st); 29 System.out.print(st +" to "+v+": "); 30 while(!path.isEmpty()) 31 { 32 System.out.print(path.pop() +" "); 33 } 34 System.out.println(); 35 } 36 public void bfs(Graph G,int w) 37 { 38 // 使用队列方式 39 Queue<VNode> queue=new LinkedList<VNode>(); 40 41 queue.add(G.graph[w]); 42 43 marked[w]=true; 44 45 while(!queue.isEmpty()) 46 { 47 VNode p=queue.poll(); 48 EdgeNode edge=p.firstedge; 49 while(edge!=null) 50 { 51 if(!marked[edge.adjvex]) 52 { 53 queue.add(G.graph[edge.adjvex]); 54 edgeTo[edge.adjvex]=p.verternum; 55 marked[edge.adjvex]=true; 56 } 57 edge=edge.nextedge; 58 } 59 60 } 61 62 } 63 public static void main(String[] args) { 64 // TODO Auto-generated method stub 65 int array[][]={{0,1},{0,2},{0,5},{1,2},{5,3},{3,2},{3,4}}; 66 int []weight={1,2,3,4,5,6,7}; 67 int []vNum={0,1,2,3,4,5}; 68 Graph G=new Graph(vNum,weight.length,array,weight); 69 G.PrintGraph(G.graph); 70 71 BreadthFirstPath bf=new BreadthFirstPath(G,0); 72 73 74 } 75 76 }
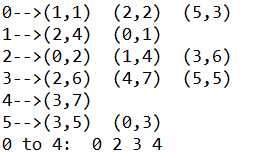
标签:read 不同 new vnode 保存 method stat bfs tac
原文地址:http://www.cnblogs.com/woainifanfan/p/6607071.html