标签：hidden 编码 blog 动态规划 idt 函数 bsp 需要 目标
摘要：
1.算法概述
2.算法推导
3.算法特性及优缺点
4.注意事项(算法过程，调参等注意事项)
5.实现和具体例子
6.适用场合
内容：
1.算法概述
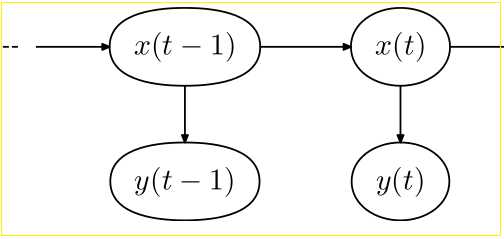
隐马尔科夫模型（Hidden Markov Model）是关于时序的概率模型，描述由一个隐含的马尔科夫链生成不可观测的状态序列，再由状态序列生成观测序列的过程。这种通过观测序列预测隐含的标记序列的问题叫做标注。
下图来自维基百科：
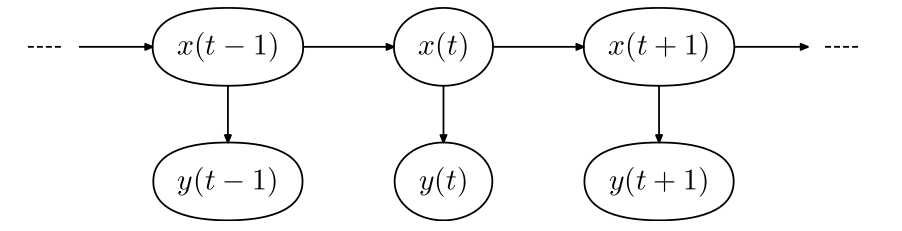
并且本文有如下符号表示：
其中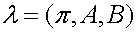
就是我们需要求得的一个三元组；拿中文分词的例子来说，分词中的状态序列是{ Begin,Middle,End,Single },对应单个字成词的就是Single,双连词就是{Begin,End},三联词就是{Begin,Middle,End}。而我们观测到的就是一个句子；通过HMM实现的分词算法可以通过
求得初始{ Begin,Middle,End,Single }这四个状态的分布，以及各个状态间相互转移的条件概率矩阵，当前状态对应一个中文词（Unicode编码）的条件概率矩阵。另一个直观的例子来自《统计学习方法》，是给定4个盒子（4个状态），每个盒子有若干红，白小球，给定一个观测序列，求对应盒子的序列。
最后马尔科夫模型的两个基本假设：
1.齐次马尔科夫假设：马尔科夫链的当前状态之和其前一刻的状态有关，与其它状态无关；对应的概率语言是：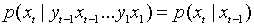
2.观测独立性假设：当前的观测只与该时刻的马尔科夫链相关，与其它观测及状态无关；对应的概率语言是：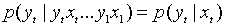
2.算法推导
以下可以看作是HMM算法的一步步拆分，并且依次加深理解：
1.在模型给定下求观测序列的概率，即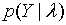
前向算法（动态规划算法）：求观测序列为y1,y2,...,yt,并且t时间点对应状态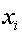
的概率
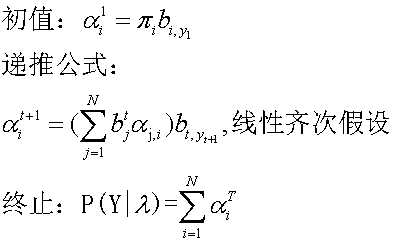
后向算法（动态规划算法）：已知t时间点对应状态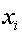，求观测序列y(t+1),y(t+2),...,y(T)的概率
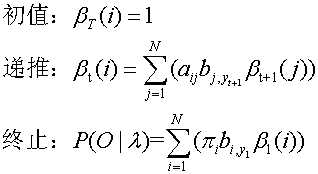
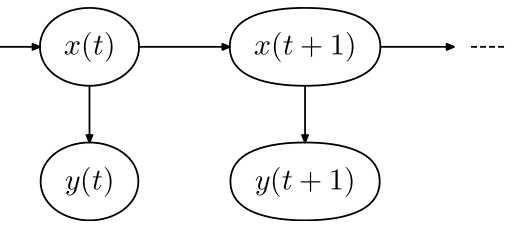
2.求解模型参数，使用对数极大似然估计，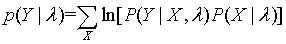
，得到三元组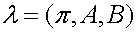
1)建立目标函数: 2)拆分三项:
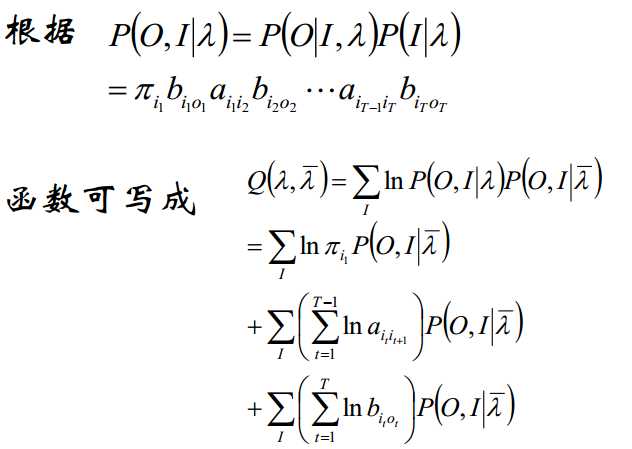
由概率加和为1，建立拉格朗日函数，求得三个最大化的
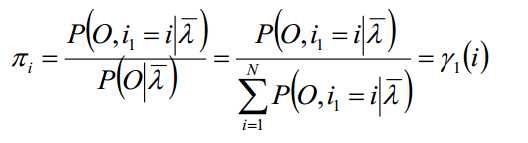
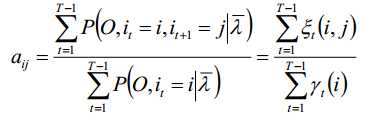
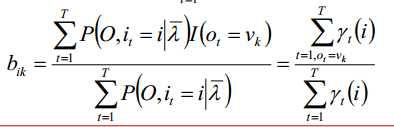
3.求最可能的状态序列，即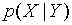
:维特比算法
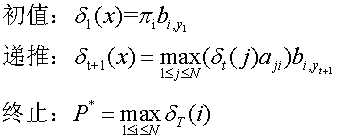
3.算法特性及优缺点 待续~~~
4.注意事项(算法过程，调参等注意事项)
5.实现和具体例子
6.适用场合
标签：hidden 编码 blog 动态规划 idt 函数 bsp 需要 目标
原文地址：http://www.cnblogs.com/arachis/p/HMM.html
