标签:for scan rac math tput sample 最优 ssi long
Description
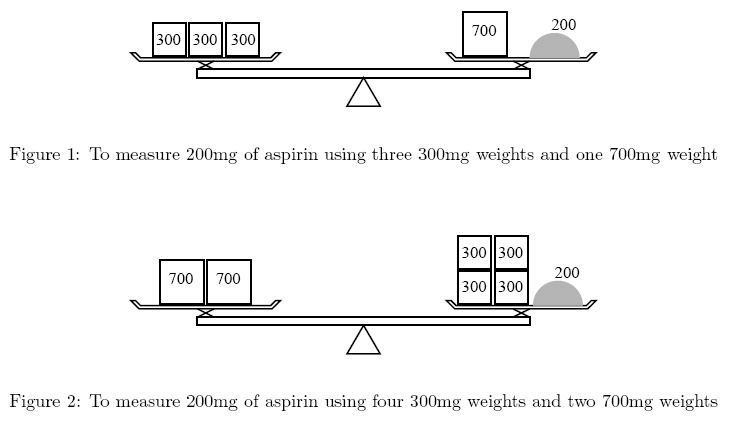
Input
Output
Sample Input
700 300 200 500 200 300 500 200 500 275 110 330 275 110 385 648 375 4002 3 1 10000 0 0 0
Sample Output
1 3 1 1 1 0 0 3 1 1 49 74 3333 1
#include<cstdio> #include<set> #include<map> #include<cstring> #include<algorithm> #include<queue> #include<iostream> #include<string> #include<cmath> #include<vector> using namespace std; typedef long long LL; /* a*x = b*y + d a*x + b*y = d |x|+|y| 的最小值 |x|+|y|==|x0+b/d*t|+|y0-a/d*t|,我们规定 a>b(如果 a<b,我们便交换 a b),从这个式子中, 我们可以轻易的发现:|x0+b/d*t|是单调递增的,|y0-a/d*t|是单调递减的,而由于我们规定了 a>b, 那么减的斜率边要大于增的斜率,于是整个函数减少的要比增加的快,但是由于绝对值的符号的作用, 最终函数还是递增的。 也就是说,函数是凹的,先减小,再增大。那么什么时候最小呢?很显然是 y0-a/d*t==0 的时候, 于是我们的最小值|x|+|y|也一定是在 t=y0*d/a附近了,只要在附近枚举几个值就能找到最优解了。 */ typedef long long LL; #define INF 0x3f3f3f3f LL ex_gcd(LL a,LL b,LL &x,LL &y) { if(b==0) { x = 1; y = 0; return a; } LL ans = ex_gcd(b,a%b,x,y); LL tmp = x; x = y; y = tmp - a/b*x; return ans; } void cal(LL a,LL b,LL c)//求ax+by==c 的一组|x|+|y| 最小的解 { bool f = false; if(a<b) { f = true; swap(a,b); } LL x=0,y=0; LL gcd = ex_gcd(a,b,x,y); x *= c/gcd; y *= c/gcd; LL t = y*gcd/a,ans=INF; LL kx,ky; for(LL i=t-1;i<=t+1;i++) { LL t1 = x + (b/gcd)*i; LL t2 = y - (a/gcd)*i; if( abs((long)t1)+abs((long)t2)<ans) { ans = abs((long)t1)+abs((long)t2); kx = (t1>0)?t1:-t1; ky = (t2>0)?t2:-t2; } } if(!f) printf("%lld %lld\n",kx,ky); else printf("%lld %lld\n",ky,kx); } int main() { LL a,b,c; while(scanf("%lld%lld%lld",&a,&b,&c),a+b+c) { cal(a,b,c); } }
标签:for scan rac math tput sample 最优 ssi long
原文地址:http://www.cnblogs.com/joeylee97/p/6661718.html