标签:时间 小根堆 blog code archive jimmy isp alt pen
左偏树是一个堆,为了实现快速合并的操作,我们可以构造一颗二叉树,并且使右子树尽量简短
什么是左偏呢?
定义:一个左偏树的外节点是一个左子树为空或者右子树为空的节点,对于每一个点定义一个距离dist它为到它子树内外节点的最短距离。
一个合法的左偏树节点需要满足堆性以及它的右子树的dist比左子树的dist小。
为什么要这样呢?
这样右子树的dist是严格控制在logn以内的。
于是我们合并的时候,将另一个左偏树与当前左偏树的右子树合并,这样递归下去,则时间复杂度是O(logn)的。
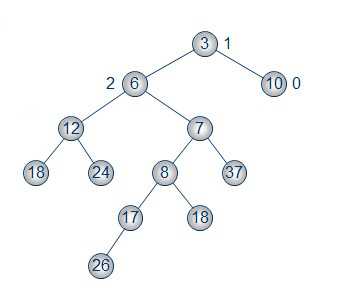
这就是一颗左偏树啦
左偏树的合并(merge)是logn的,merge用图解比较好说
P.S.:图解是小根堆,模板代码是大根堆
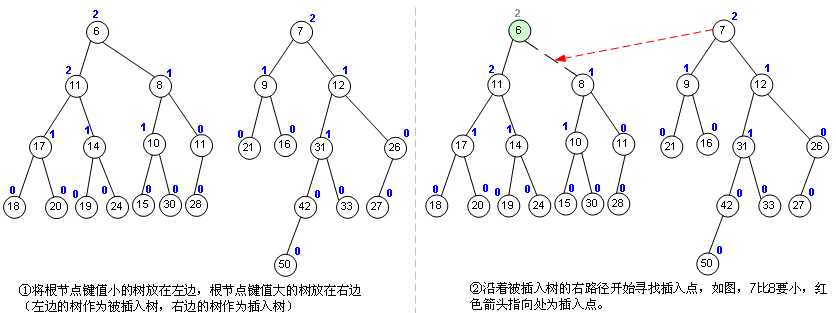
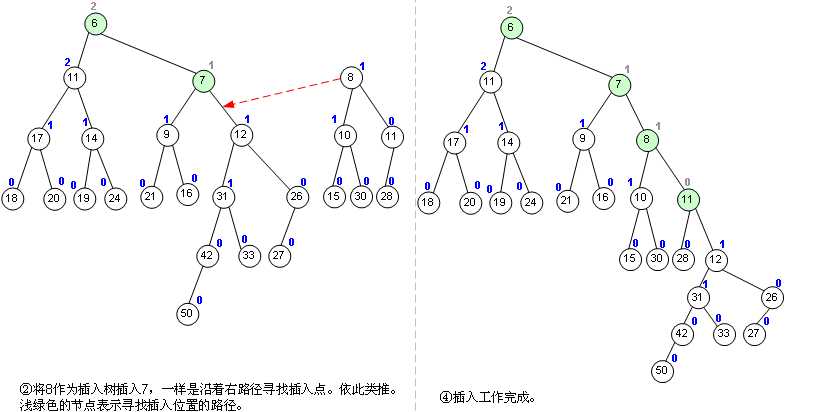
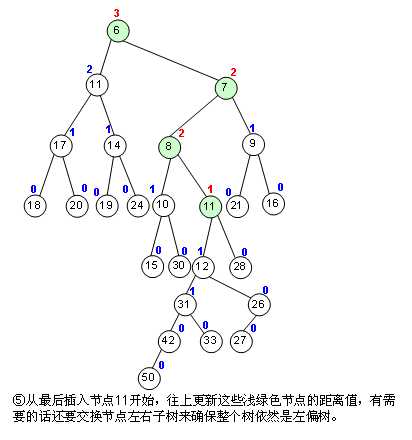
代码操作:insert(int x,int y) 在编号为x的左偏树里插入权值为y的新节点
top(int x) 返回编号为x的左偏树的堆顶的权值
pop(int x) 删除编号为x的左偏树的堆顶,返回新的堆顶编号
mergg(int x,int y)合并编号为x,y的两颗左偏树

#include<iostream> #include<cstdlib> #include<cstdio> #include<algorithm> #define N 3010 using namespace std; int tot; struct big_heap{ int l,r,d,w; }h[N]; inline int init(int x){ tot++; h[tot].w=x; h[tot].l=h[tot].r=h[tot].d=0; return tot; } inline insert(int x,int y){ return merge(x,init(y)); } inline int pop(int x){ int l=h[x].l,r=h[x].r; h[x].l=h[x].r=h[x].w=0; return merge(l,r); } inline int top(int x){ return h[x].w; } inline int merge(int x,int y){ if(!x) return y; if(!y) return x; if(h[x].w<h[y].w) swap(x,y); //保证大根堆性质 h[x].r=merge(h[x].r,y); //合并 if(h[h[x].l].d<h[h[x].r].d) swap(h[x].l,h[x].r); //保证左偏性质 h[x].d=h[h[x].r].d+1; //更新深度 return x; } inline void Jimmy(){ } int main(){ Jimmy(); return 0; }
本篇有关博客链接:
http://www.cnblogs.com/crazyac/articles/1970176.html
http://www.cnblogs.com/yc_sunniwell/archive/2010/06/28/1766756.html
http://aireenye.leanote.com/post/Left-Tree
// orz Aireen
标签:时间 小根堆 blog code archive jimmy isp alt pen
原文地址:http://www.cnblogs.com/JimmyC/p/6664012.html