标签:tree 中序 == 赋值 color amp 技术分享 ios 比较
如题,给出二叉树的前序遍历和中序遍历,怎么还原二叉树。
假如一个二叉树的前序遍历为:12453,中序遍历为:42513。由于这颗二叉树比较简单,可以用 凑 的方法很容易凑出符合题意的二叉树(没有写这篇文章之前,我都是用这种笨方法的..尴尬)。
即如图:
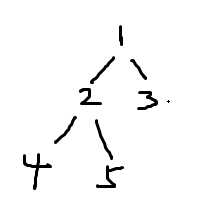
那么有没有一个标准的方法来推导呢?当然是有的!
我们来分析一下这棵树的前序和中序。
先看前序:12453,第一个字符“1”肯定是整棵树root节点,这不用解释。至于第二个字符以及往后的字符就没有什么可用的信息了。
再看中序:42513,前序中只有“1”这个节点有用,我们在中序中找到“1”的位置,然后再对照上面的图,会发现在“1”左边的所有字符是“1”这个节点的左子树,“1”右边的所有字符是“1”这个节点的右子树。
既然知道了“1”这个节点的左右子树,那么我们可以先把“1”这个节点忽略掉,再分别求“1”这个节点 左右子树 的root节点。
先求“1”的左子树的root节点:
先找到“1”的左子树的中序:42513 --> 425,然而并没有什么有用的信息。
再找到“1”的左子树的前序:12453 --> 245,我们刚才说过前序遍历的第一个字符肯定是它所在的树的root节点。即“2”是 “1”的左子树245的 root节点。
接下来求“1”的右子树的root节点:
先找到“1”的右子树的中序:42513 --> 3,只有一个节点。
再找到“1”的右子树的前序:12453 --> 3,只有一个节点,那么“3”是“1”的右子树的root节点。
知道了“1”和“2”是root节点,再把“2”忽略掉,分别求“2”这个节点的 左右子树的 root节点。
求“2”的左子树的root节点:
“2”的左子树的中序:425 --> 4,“4”为其左子树。
“2”的左子树的前序:245 --> 4,可以确认“4”为当前子树的root节点。
求“2”的右子树的root节点:
“2”的右子树的中序:425 --> 5,“5”为其右子树。
“2”的右子树的前序:245 --> 5,可以确认“5”为当前子树的root节点。
看到这里你应该会明白:中序用来找某个节点的左右子树,前序用来找某个子树的root节点。其中,当某个子树长度为0时,root=NULL,返回。
根据这个规律:我们可以递归地找到所有子树的root节点,那么这棵树各个节点的相对位置也就确认了。
代码实现方法:
#include <iostream> #include <cstring> using namespace std; //先定义二叉树节点结构体 typedef struct Bitree { char data; struct Bitree *lchild; struct Bitree *rchild; }BiTree; //第一种建树方式,传入节点指针 这里的len参数指的是mid数组的结尾下标。当len为0时,代表有一个节点。 void buildTree(BiTree *&node,char *pre,char *mid,int len) { if(len<0) //当结尾下标<0时,没有子树 { node=NULL; return; } for(int i=0;i<=len;i++) //遍历mid数组找到子树的root节点 并为其分配空间,赋值。 { if(pre[0]==mid[i]) //中序遍历中找到root节点(前序第一个字符就是root节点) { node=new BiTree; node->data=pre[0]; buildTree(node->lchild,pre+1,mid,i-1); //递归地找左子树的root节点 buildTree(node->rchild,pre+i+1,mid+i+1,len-i-1); //递归地找右子树的root节点 } } } //第二种建树方法,函数返回节点指针 BiTree* buildTree2(char *pre,char *mid,int len) { BiTree *node; for(int i=0;i<=len;i++) { if(pre[0]==mid[i]) { node=new BiTree; node->data=pre[0]; node->lchild=buildTree2(pre+1,mid,i-1); node->rchild=buildTree2(pre+i+1,mid+i+1,len-i-1); return node; } } return NULL; } void preOrder(BiTree *node) //前序遍历输出二叉树 { if(node) { cout<<node->data; preOrder(node->lchild); preOrder(node->rchild); } } void midOrder(BiTree *node) //中序遍历输出二叉树 { if(node) { preOrder(node->lchild); cout<<node->data; preOrder(node->rchild); } } int main() { char pre[]="12453"; //前序遍历 char mid[]="42513"; //中序遍历 BiTree *root; //buildTree(root,pre,mid,4); root=buildTree2(pre,mid,4); preOrder(root); cout<<endl; midOrder(root); return 0; }
标签:tree 中序 == 赋值 color amp 技术分享 ios 比较
原文地址:http://www.cnblogs.com/f-society/p/6668228.html