标签:strong ora zed span 迭代 圣经 步骤 name chain
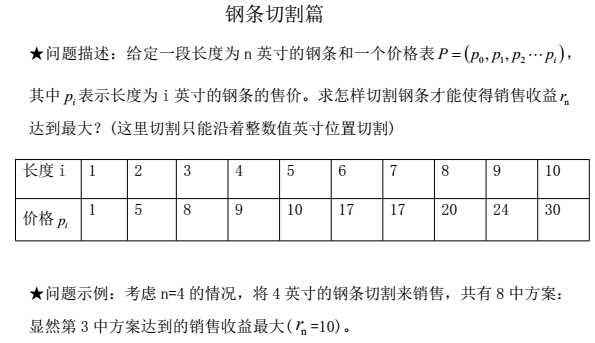
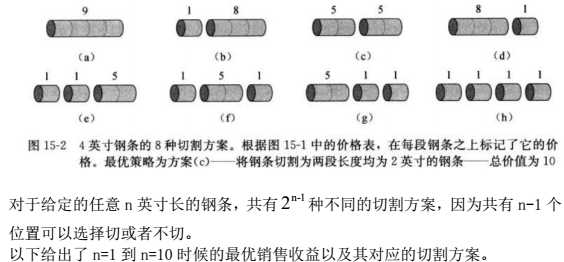
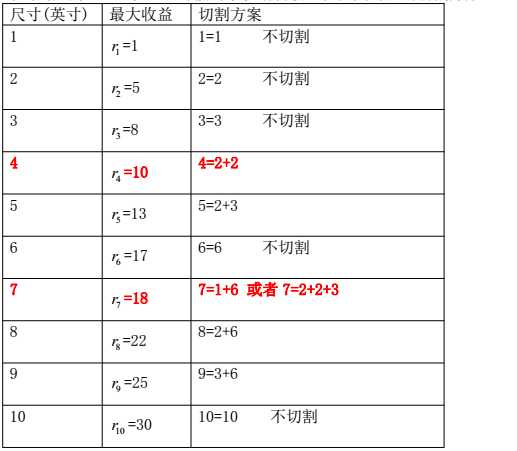
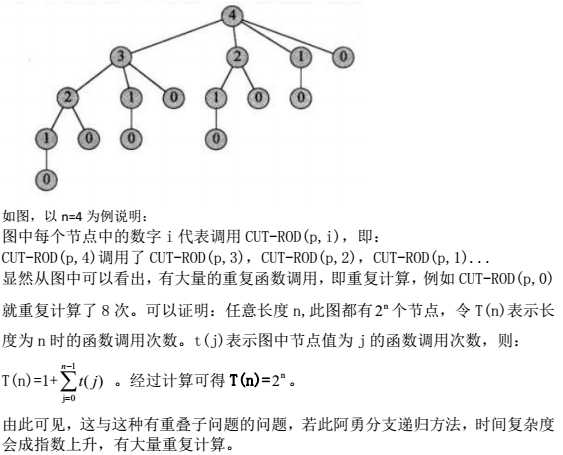
本文以两个具体例子详细剖析动态规划算法设计思想,主要参考圣经《算法导论》,加上自己的一些理解,主要是附上了一些具体实现过程,所以希望能对大家有所帮助。




#_*_ coding:utf-8 _*_
import numpy as np
def MemoizedCutRodAux(p,n,r,s):
if r[n]>=0:
return r[n]
if n==0:
q=0
c=0
else:
q=-1
c=-1
for i in range(1,n+1):
if q<(p[i]+MemoizedCutRodAux(p,n-i,r,s)):
q=p[i]+MemoizedCutRodAux(p,n-i,r,s)
c=i
r[n]=q
s[n]=c
return q
def MemoizedCutRod(p,n):
r=-np.ones(n+1)
s = -np.ones(n + 1)
MemoizedCutRodAux(p,n,r,s)
return r,s
if __name__==‘__main__‘:
p=np.array([0,1,5,8,9,10,17,17,20,24,30])
r,s=MemoizedCutRod(p, 10)
print r
print s
结果输出:
r=[ 0. 1. 5. 8. 10. 13. 17. 18. 22. 25. 30.]
s=[ 0. 1. 2. 3. 2. 2. 6. 1. 2. 3. 10.]



import numpy as np
def BottomUpCutRod(p,n):
r = -np.ones(n + 1)
s = -np.ones(n + 1)
r[0]=0
s[0]=0
q=-1
for j in range(1,n+1):
for i in range(1,j+1):
if q<(p[i]+r[j-i]):
q=p[i]+r[j-i]
s[j]=i
r[j]=q
return r,s
if __name__==‘__main__‘:
p = np.array([0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30])
r,s= BottomUpCutRod(p,10)
print r
print s





★步骤三:采用自底向上迭代法计算最优解的值
import numpy as np
def MatrixChain(p):
n=p.size-1
m=np.ones((n+1,n+1))*np.inf
s = np.zeros((n+1, n+1))
for i in range(n+1):
m[i,i]=0
for lenth in range(2,n+1):
for i in range(1,n-lenth+2):
j=i+lenth-1
for k in range(i,j):
q=m[i,k]+m[k+1,j]+p[i-1]*p[k]*p[j]
if q<m[i,j]:
m[i,j]=q
s[i,j]=k
return m,s
if __name__==‘__main__‘:
p=np.array([50,10,40,30,5])
m,s=MatrixChain(p)
print m
print s
结果输出:
m=[[ 0. inf inf inf inf]
[ inf 0. 20000. 27000. 10500.]
[ inf inf 0. 12000. 8000.]
[ inf inf inf 0. 6000.]
[ inf inf inf inf 0.]]
s=[[ 0. 0. 0. 0. 0.]
[ 0. 0. 1. 1. 1.]
[ 0. 0. 0. 2. 2.]
[ 0. 0. 0. 0. 3.]
[ 0. 0. 0. 0. 0.]]


----------------------------------------------------------------------------------------------
本文为作者原创,其中代码都是可以运行通过(Python),希望有所帮助
标签:strong ora zed span 迭代 圣经 步骤 name chain
原文地址:http://www.cnblogs.com/xiaotan-code/p/6674984.html