标签:斐波那契数列 fibonacii mat lan color out 推导 img ima
第一讲、Fibonacii

1 //斐波那契递归求解 2 #include<iostream> 3 #include<cstdio> 4 #include<cstdlib> 5 using namespace std; 6 int f(int x) 7 { 8 if(x==1||x==2)return 1; 9 else 10 return f(x-1)+f(x-2); 11 } 12 int main() 13 { 14 int n; 15 scanf("%d",&n); 16 printf("%d",f(n)); 17 return 0; 18 }
(2)

1 //求斐波那契数列(通项公式) 2 #include<iostream> 3 #include<cstdio> 4 #include<cmath> 5 using namespace std; 6 int main() 7 { 8 int n; 9 scanf("%d",&n); 10 double x=sqrt(5.0); 11 int ans=(pow((1+x)/2,n)-pow((1-x)/2,n))*x/5; 12 printf("%d",ans); 13 return 0; 14 }
练习:
(1)
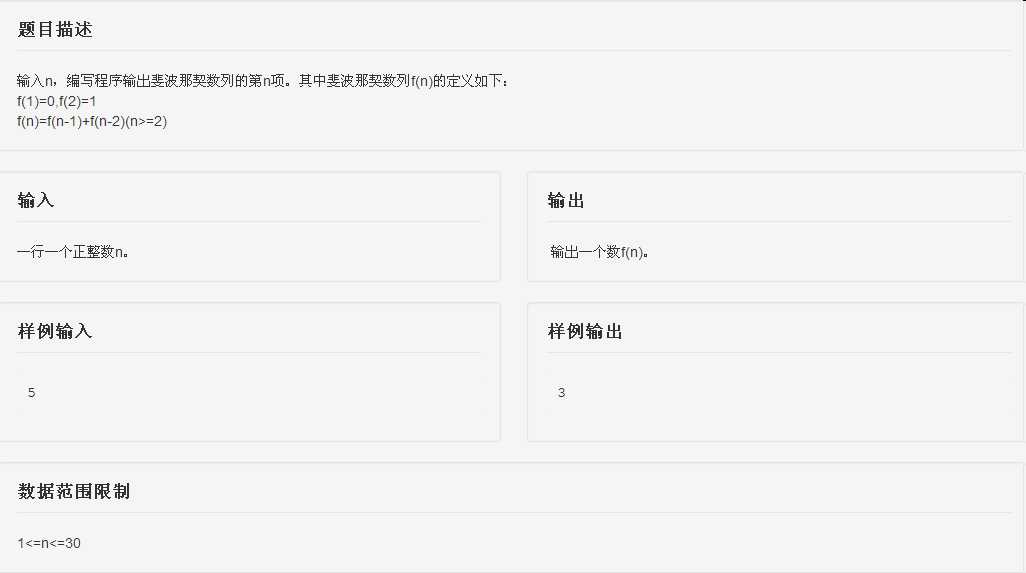
(代码上面有)
(2)
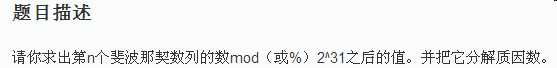

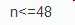

1 //第n个斐波那契数列%pow(2,31)的值 2 #include<iostream> 3 #include<cstdio> 4 #include<cmath> 5 using namespace std; 6 int main() 7 { 8 int n; 9 scanf("%d",&n); 10 double x=sqrt(5.0); 11 long long ans=(pow((1+x)/2,n)-pow((1-x)/2,n))*x/5; 12 long long m=pow(2,31); 13 ans%=m; 14 printf("%d\n",ans); 15 printf("%d=",ans); 16 int number=2,count=0; 17 while(ans!=1) 18 { 19 if(ans%number) 20 number++; 21 else 22 { 23 count++; 24 if(count==1)printf("%d",number); 25 else 26 printf("*%d",number); 27 ans/=number; 28 } 29 } 30 return 0; 31 }
(3)
codevs 2834

1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 int f[2000]; 5 int main() 6 { 7 int n,p,x; 8 scanf("%d%d%d",&n,&p,&x); 9 f[1]=f[2]=1; 10 for(int i=3;i<=1000;i++) 11 { 12 f[i]=f[i-1]+f[i-2]; 13 f[i]%=p; 14 } 15 for(int i=1;i<=x;i++) 16 { 17 if(f[i]==n) 18 {cout<<i; 19 return 0; 20 } 21 } 22 cout<<-1; 23 return 0; 24 }
快速幂取模的模板

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 using namespace std; 5 int f(int x,int n) 6 { 7 int now=1; 8 while(n) 9 { 10 if(n&1) 11 { 12 now=now*x; 13 } 14 x=x*x; 15 n>>=1; 16 } 17 return now; 18 } 19 int main() 20 { 21 int x,n; 22 cin>>x>>n; 23 cout<<f(x,n); 24 return 0; 25 }
标签:斐波那契数列 fibonacii mat lan color out 推导 img ima
原文地址:http://www.cnblogs.com/zzyh/p/6679655.html