[POJ 1308]Is It A Tree?(并查集判断图是否为一棵有根树)

标签：des   style   blog   http   color   os   io   for   ar   

Description

A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.

There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.

In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.

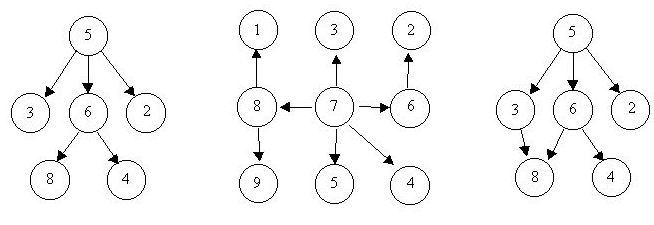
Input

Output

Sample Input

6 8  5 3  5 2  6 4
5 6  0 0

8 1  7 3  6 2  8 9  7 5
7 4  7 8  7 6  0 0

3 8  6 8  6 4
5 3  5 6  5 2  0 0
-1 -1

Sample Output

Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.

Source

完全看不到并查集的影子了。。。此题就是拿并查集父子节点的关系来模拟一个图，在输入过程中，如果一个子节点被多个父节点连接，或一个节点的边自己指向自己，则可直接判定不是有根树，若输入过程中不能直接判定，整个图的父子关系建立完成后，也可通过并查集查找每个节点的根节点来判定是否为有根树，若每个节点的根节点有不同的，则表明此图有多个根节点，不是有根树，若并查集查找过程中递归次数超过一定大小(1000)，则可视作为死循环，表明图中有环，也可判定不是有根树。此题的判定限制条件很多，千万不能有漏掉的。

#include <iostream>

#define MAXN 1010

using namespace std;

struct Node
{
    int f,used; //f=父节点，used=1表示该点已经和其他点连接上了
}node[MAXN];

void MakeSet()
{
    for(int i=0;i<MAXN;i++)
    {
        node[i].f=0;
        node[i].used=0;
    }
}

int findSet(int num,int step)
{
    if(step>1000) return -5; //为环
    if(node[num].f==0) return num;
    return findSet(node[num].f,step+1);
}

void AddEdge(int a,int b) //建立有向边a->b
{
    node[a].used=1;
    node[b].used=1;
    node[b].f=a;
}

int main()
{
    int s,t,CASE=0;
    while(1)
    {
        bool isTree=true;
        CASE++;
        MakeSet();
        while(cin>>s>>t&&s>0)
        {
            if(s==t) isTree=false;
            else if(node[t].f==0) AddEdge(s,t); //子节点t没有和其他点连接，可以加新边
            else isTree=false; //否则子节点t已经和其他点连接，不是树
        }
        if(s==0)
        {
            if(!isTree) //已经确定不是一棵有根树
            {
                cout<<"Case "<<CASE<<" is not a tree."<<endl;
                continue;
            }
            int root=0,times=0;
            for(int i=1;i<1000;i++)
            {
                if(node[i].used==1) //点i和其他边连接
                {
                    if(times==0) //第一次查找
                        root=findSet(i,1); //确定一个根节点root
                    else if(root!=findSet(i,1)||findSet(i,1)<0||root<0) //如果点i的根节点不是之前确定的根节点(有多个根节点)，或存在环，则不是树
                    {
                        isTree=false;
                        break; //不用再找了
                    }
                    times++;
                }
            }
            if(isTree) cout<<"Case "<<CASE<<" is a tree."<<endl;
            else cout<<"Case "<<CASE<<" is not a tree."<<endl;
        }
        else break;
    }
    return 0;
}

[POJ 1308]Is It A Tree?(并查集判断图是否为一棵有根树)

标签：des   style   blog   http   color   os   io   for   ar   

原文地址：http://blog.csdn.net/qpswwww/article/details/38779693