标签：contain about main rri function span scan test maximum
Something happened in Uzhlyandia again... There are riots on the streets... Famous Uzhlyandian superheroes Shean the Sheep and Stas the Giraffe were called in order to save the situation. Upon the arriving, they found that citizens are worried about maximum values of the Main Uzhlyandian Function f, which is defined as follows:
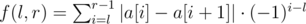
In the above formula, 1?≤?l?<?r?≤?n must hold, where n is the size of the Main Uzhlyandian Array a, and |x| means absolute value of x. But the heroes skipped their math lessons in school, so they asked you for help. Help them calculate the maximum value of f among all possible values of l and r for the given array a.
The first line contains single integer n (2?≤?n?≤?105) — the size of the array a.
The second line contains n integers a1,?a2,?...,?an (-109?≤?ai?≤?109) — the array elements.
Print the only integer — the maximum value of f.
5
1 4 2 3 1
3
4
1 5 4 7
6
In the first sample case, the optimal value of f is reached on intervals [1,?2] and [2,?5].
In the second case maximal value of f is reachable only on the whole array.
题意：给你一个长度为n的序列，问你在 l 与 r 取不同值时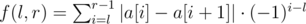最大值是多少？
思路：能够看出这就是在abs（a[i]-a[i+1]）取正负正负···和取负正负正···然后求子序列的最大值
AC代码：
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int maxn=100005; 4 long long a[maxn],b[maxn],c[maxn]; 5 int main() 6 { 7 8 int n; 9 while(~scanf("%d",&n)) 10 { 11 for(int i=0; i<n; i++) 12 { 13 scanf("%I64d",&c[i]); 14 } 15 for(int i=0; i<n-1; i++) 16 { 17 if(i%2==0) 18 { 19 a[i]=abs(c[i]-c[i+1]); 20 b[i]=-a[i]; 21 } 22 else 23 { 24 b[i]=abs(c[i]-c[i+1]); 25 a[i]=-b[i]; 26 } 27 } 28 long long ans=0,num=0; 29 for(int i=0; i<n-1; i++) 30 { 31 num+=a[i]; 32 if(num>ans) 33 { 34 ans=num; 35 } 36 else if(num<0) 37 { 38 num=0; 39 } 40 } 41 num=0; 42 for(int i=0; i<n-1; i++) 43 { 44 num+=b[i]; 45 if(num>ans) 46 { 47 ans=num; 48 } 49 else if(num<0) 50 { 51 num=0; 52 } 53 } 54 printf("%I64d\n",ans); 55 } 56 return 0; 57 }
Codeforces Round #407 (Div. 2) C Functions again（最大子序列和）
标签：contain about main rri function span scan test maximum
原文地址：http://www.cnblogs.com/wang-ya-wei/p/6686108.html
