标签：style   blog   http   2014   问题   log   line   sp   ad   

前言

说到集合就不得不提到康拓，虽说集合论对现代数学有着非常大的影响，但总是对他的无限集的理论有一些疑问（不知道是不是叫无限集，反正我是这么叫）。最简单的例子就是一个平面上点的数量与一条直线上点的数量一样多（这是人第一次听到都会觉得不对吧）。该问题普遍的解释一般是说这两者的元素之间有一一对应的关系（好比是你有啥我就有啥）。所以我就针对这个问题发表来一个奇葩的悖论。

主干

首先我们来看一下圆锥与圆柱。小学里就知道圆锥的体积是圆柱的1/3，可换一个角度想想，如果都把圆锥与圆柱沿水平方向切成无限份，那么对于圆锥上的某一切片是否可以对应到圆柱上的某一切片呢。这样说可能太抽象，不如再换一个直观的例子：

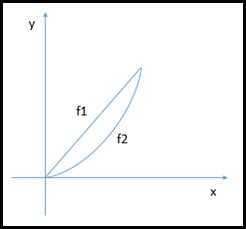如图所示，该图为两个函数的某一部分，且两端点重合。现要询问两个函数各自的Y值之和谁大谁小

 给出两种思路：

 从x的角度去看，对于任意一个在范围中的x，除端点外，f1均大于f2。因此f1的Y值之和更大。

 从y的角度去看，对于任意一个在范围中的y，必有点x1，使其函数值f1与y相等（f2同理）。因此，两者的Y值之和相等。

 怎么样是不是感觉有点不对了呀

一个奇葩的悖论

标签：style   blog   http   2014   问题   log   line   sp   ad   

原文地址：http://www.cnblogs.com/zhu8655/p/3931806.html